题目内容
设数列{an}是等差数列,若a3+a4+a5=12,则a1+a2+…+a7= .
考点:等差数列的性质
专题:计算题,等差数列与等比数列
分析:由a3+a4+a5=12,可得 a4=4,故有 a1+a2+…+a7=7a4,运算求得结果.
解答:
解:∵数列{an}是等差数列,a3+a4+a5=12,
∴3a4=12,
∴a4=4.
∴a1+a2+…+a7=7a4=28.
故答案为:28.
∴3a4=12,
∴a4=4.
∴a1+a2+…+a7=7a4=28.
故答案为:28.
点评:本题主要考查等差数列的定义和性质,属于基础题.

练习册系列答案
相关题目
已知f(α)=
.
(1)化简f(α);
(2)若f(α)=
,且
<α<
,求cosα-sinα的值.
| sin(π-α)•cos(2π-α)•tan(-π+α) |
| sin(-π+α)•tan(-α+3π) |
(1)化简f(α);
(2)若f(α)=
| 1 |
| 8 |
| π |
| 4 |
| π |
| 2 |
已知x∈(0,
)且f(cosx)=sin
,则f(
)=( )
| π |
| 2 |
| x |
| 2 |
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
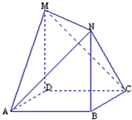 四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=1.
四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=1.