题目内容
已知x∈(0,
)且f(cosx)=sin
,则f(
)=( )
| π |
| 2 |
| x |
| 2 |
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:函数的值
专题:函数的性质及应用
分析:根据函数的表达式,直接进行转化即可进行求解.
解答:
解:∵当x∈(0,
),cos
=
,
∴f(
)=f(cos
)=sin
=sin
=
,
故选:C.
| π |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
∴f(
| 1 |
| 2 |
| π |
| 3 |
| ||
| 2 |
| π |
| 6 |
| 1 |
| 2 |
故选:C.
点评:本题主要考查函数值的计算,将条件进行转化是解决本题的关键,比较基础.

练习册系列答案
相关题目
若tan280°=a,则sin80°的结果为( )
A、-
| ||||
B、
| ||||
C、-
| ||||
D、-
|
在△ABC中,a=2,b=
,A=
,则B等于( )
| 2 |
| π |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在等比数列{an}中,Sn是它的前n项和,若a2•a3=2a1,且a4与2a7的等差中项为17,则S6=( )
A、
| ||
| B、16 | ||
| C、15 | ||
D、
|
下列命题中,与命题“函数y=
的定义域为R”不等价的命题是( )
| ax2+bx+c |
| A、函数y=ax2+bx+c的最小值大于0 |
| B、不等式ax2+bx+c≥0对任意实数恒成立 |
| C、不存在x0∈R,使ax02+bx0+c<0 |
| D、函数y=ax2+bx+c的值域是[0,+∞)的子集 |
为了解本市的交通状况,某校高一年级的同学分成了甲、乙、丙三个组,从下午13点到18点,分别对三个路口的机动车通行情况进行了实际调查,并绘制了频率分布直方图(如图),记甲、乙、丙三个组所调查数据的标准差分别为s1,s2,s3,则它们的大小关系为( )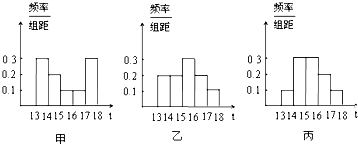

| A、s1>s2>s3 |
| B、s1>s3>s2 |
| C、s2>s3>s1 |
| D、s3>s2>s1 |
要得到一个偶函数的图象,只需将函数f(x)=sin(x-
)的图象( )
| π |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|