题目内容
7.在极坐标系中,已知圆C圆心的极坐标为($\sqrt{2}$,$\frac{π}{4}$),半径为$\sqrt{3}$.(1)求圆C的极坐标方程;
(2)以极点为原点,以极轴为x轴正半轴建立直角坐标系,已知直线l的参数方程为$\left\{\begin{array}{l}{x=2+tcosα}\\{y=2+tsinα}\end{array}\right.$(t为参数),直线l交圆C于A、B两点,且|AB|∈[2$\sqrt{2}$,2$\sqrt{3}$),求直线l的斜率k的取值范围.
分析 (1)圆C圆心的极坐标为($\sqrt{2}$,$\frac{π}{4}$),化为直角坐标:C(1,1),半径为$\sqrt{3}$.直角坐标方程为:(x-1)2+(y-1)2=3,利用$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$即可得出极坐标方程.
(2)直线l的参数方程为$\left\{\begin{array}{l}{x=2+tcosα}\\{y=2+tsinα}\end{array}\right.$(t为参数),代入圆的方程可得:t2+(2cosα+2sinα)t-1=0,利用|AB|=|t1-t2|=$\sqrt{({t}_{1}+{t}_{2})^{2}-4{t}_{1}{t}_{2}}$∈[2$\sqrt{2}$,2$\sqrt{3}$),即可得出.
解答 解:(1)圆C圆心的极坐标为($\sqrt{2}$,$\frac{π}{4}$),化为直角坐标:C(1,1),半径为$\sqrt{3}$.
∴直角坐标方程为:(x-1)2+(y-1)2=3,化为x2+y2-2x-2y=1,化为极坐标方程:ρ2-2ρcosθ-2ρsinθ=1.
(2)直线l的参数方程为$\left\{\begin{array}{l}{x=2+tcosα}\\{y=2+tsinα}\end{array}\right.$(t为参数),代入圆的方程可得:(1+tcosα)2+(1+tsinα)2=3,
化为:t2+(2cosα+2sinα)t-1=0,
∴t1+t2=-(2cosα+2sinα),t1t2=-1,
∴|AB|=|t1-t2|=$\sqrt{({t}_{1}+{t}_{2})^{2}-4{t}_{1}{t}_{2}}$=$\sqrt{(2cosα+2sinα)^{2}+4}$=$\sqrt{8+8sinαcosα}$∈[2$\sqrt{2}$,2$\sqrt{3}$),
∴0≤sinαcosα$<\frac{1}{2}$,
解得:0≤tanα<1.
∴直线l的斜率k的取值范围是[0,1).
点评 本题考查了极坐标方程化为直角坐标方程、参数方程化为普通方程、弦长问题,考查了推理能力与计算能力,属于中档题.

 名校课堂系列答案
名校课堂系列答案| A. | l垂直于平面α内的一条直线 | B. | l垂直于平面α内的两条直线 | ||
| C. | l垂直于平面α内的无数条直线 | D. | l垂直于平面α内的任一条直线 |
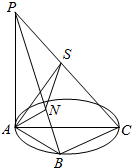 如图,AC为圆O的直径,B为圆周上不与点A、C重合的点,PA垂直于圆O所在的平面,连结PB、PC、AB、BC,作AN⊥PB,AS⊥PC,连结SN,则图中直角三角形个数为( )
如图,AC为圆O的直径,B为圆周上不与点A、C重合的点,PA垂直于圆O所在的平面,连结PB、PC、AB、BC,作AN⊥PB,AS⊥PC,连结SN,则图中直角三角形个数为( )| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
| A. | 偶函数且增函数 | B. | 偶函数且减函数 | C. | 奇函数且增函数 | D. | 奇函数且减函数 |