题目内容
19.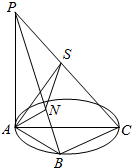 如图,AC为圆O的直径,B为圆周上不与点A、C重合的点,PA垂直于圆O所在的平面,连结PB、PC、AB、BC,作AN⊥PB,AS⊥PC,连结SN,则图中直角三角形个数为( )
如图,AC为圆O的直径,B为圆周上不与点A、C重合的点,PA垂直于圆O所在的平面,连结PB、PC、AB、BC,作AN⊥PB,AS⊥PC,连结SN,则图中直角三角形个数为( )| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
分析 分别根据线面垂直的判定定理和性质定理分别进行证明线线垂直的关系,最后综合讨论结果,可得答案.
解答  解:∵AC是⊙O的直径,
解:∵AC是⊙O的直径,
∴AB⊥BC,可得:△ABC为直角三角形,
∵PA⊥⊙O所在平面,
∴PA⊥⊙O所在平面内的所有直线,
∴PA⊥AC,PA⊥AB,PA⊥BC,可得:△PAB、△PAC为直角三角形,
又∵AB∩AP=A,AB,AP?平面PAB,∴BC⊥面PAB,
又∵PB?平面PAB,∴BC⊥PB,可得:△PCB为直角三角形,
∵AS⊥PC,可得:△PAS、△ASC为直角三角形,
∴AN⊥PB,可得:△PAN、△ABN为直角三角形,
∵AN⊥BC,AN⊥PB,BC∩PB=B,可得:AN⊥平面PBC,可得:AN⊥SN,即:△ANS为直角三角形,
∵AN⊥平面PBC,可得:AN⊥PC,又AC⊥PC,可得PC⊥平面ANS,可得:PC⊥SN,可得:△PSN为直角三角形,
综上,则图中直角三角形个数为10个.
故选:D.
点评 本题主要考查了直线与平面垂直的判定,以及直线与平面垂直的性质,考查化归与转化的数学思想方法,属于中档题.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
9.若函数f(x)满足f(x)=x2lnx+3xf′(1)-1,则f′(1)等于( )
| A. | -$\frac{1}{2}$ | B. | -$\frac{1}{3}$ | C. | -1 | D. | 1 |
4.(x2+2)(x-$\frac{1}{x}$)6的展开式中常数项为( )
| A. | -40 | B. | -25 | C. | 25 | D. | 55 |
11.在△ABC中,a=7,b=14,A=30°,则此三角形解的情况是( )
| A. | 一解 | B. | 两解 | C. | 一解或两解 | D. | 无解 |
9.已知△ABC中,(a+b+c)(sinA+sinB-sinC)=asinB,其中A,B,C为△ABC的内角,a,b,c分别为A,B,C的对边,则C=( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{3π}{4}$ | D. | $\frac{5π}{6}$ |