题目内容
18．命题p：实数x满足$\frac{x+m}{x+3m}$＜0，其中m＜0；命题q：实数x满足x2-x-6＜0或x2+2x-8＜0，且￢p是￢q的必要不充分条件，求m的取值范围．分析 分别解出命题p，q的解集A，B．由于￢p是￢q的必要不充分条件，等价于q是p的必要不充分条件，即A是B的真子集，即可得出．
解答 解：对于命题P：实数x满足$\frac{x+m}{x+3m}$＜0，其中m＜0，∴（x+m）（x+3m）＜0，解得-m＜x＜-3m，可得A=（-m，-3m）．
对于命题q：实数x满足x2-x-6＜0或x2+2x-8＜0，解得-2＜x＜3，或-4＜x＜2，可得解集B=（-4，3）．
∵￢p是￢q的必要不充分条件，等价于q是p的必要不充分条件，
∴A是B的真子集，
∴-3m≤3，则m≥-1，又m＜0．
∴m∈[-1，0）．
点评 本题考查了简易逻辑的判定方法、集合的运算性质、不等式的解法，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
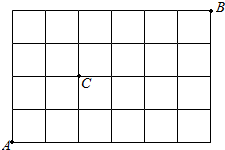
8．如图，某地区有7条南北向街道，5条东西街道，从A点走向B点最短的走法中，必须经过C点的概率（ ）
| A． | $\frac{3}{7}$ | B． | $\frac{6}{7}$ | C． | $\frac{3}{10}$ | D． | $\frac{7}{10}$ |
9．若函数f（x）满足f（x）=x2lnx+3xf′（1）-1，则f′（1）等于（ ）
| A． | -$\frac{1}{2}$ | B． | -$\frac{1}{3}$ | C． | -1 | D． | 1 |
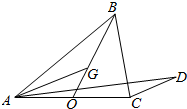如图，在△ABC中，BO为边AC上的中线，$\overrightarrow{BG}=2\overrightarrow{GO}$，设$\overrightarrow{CD}$∥$\overrightarrow{AG}$，若$\overrightarrow{AD}=\frac{1}{5}\overrightarrow{AB}+λ\overrightarrow{AC}$（λ∈R），则λ的值为（ ）