函数f均是连续函数.若${∫} {1}^{2}$g(x)dx=3.${∫} {0}^{2}$f(x)dx=1.${∫} {0}^{1}$f(x)dx=-2.则${∫} {1}^{2}$[f]dx=6．题目和参考答案——青夏教育精英家教网—

题目内容

15．函数f（x），g（x）均是连续函数，若${∫}_{1}^{2}$g（x）dx=3，${∫}_{0}^{2}$f（x）dx=1，${∫}_{0}^{1}$f（x）dx=-2，则${∫}_{1}^{2}$[f（x）+g（x）]dx=6．

分析由题意和定积分的运算性质可得原式=${∫}_{0}^{2}$f（x）dx-${∫}_{0}^{1}$f（x）dx+${∫}_{1}^{2}$g（x）dx，代值计算可得．

解答解：由题意可得${∫}_{1}^{2}$[f（x）+g（x）]dx=${∫}_{1}^{2}$f（x）dx+${∫}_{1}^{2}$g（x）dx
=${∫}_{0}^{2}$f（x）dx-${∫}_{0}^{1}$f（x）dx+${∫}_{1}^{2}$g（x）dx=1-（-2）+3=6
故答案为：6

点评本题考查定积分的运算性质，属基础题．

练习册系列答案

相关题目

5．

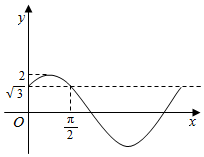设函数f（x）=Asin（ωx+φ）（A，ω＞0，0＜|φ|＜π）在一个周期内的图象如图所示．
（1）求函数f（x）的解析式；
（2）求g（x）=f（3x+$\frac{π}{4}$）-1在[-$\frac{π}{6}$，$\frac{π}{3}$]上的值域．

6．已知曲线C₁的参数方程为$\left\{\begin{array}{l}{x=2-t}\\{y=\sqrt{3}t}\end{array}\right.$（t为参数），当t=-1时，对应曲线C₁上一点A且点A关于原点的对称点为B，以原点O为极点，以x轴为正半轴为极轴建立坐标系，曲线C₂的极坐标方程为ρ=$\frac{6}{\sqrt{9-3si{n}^{2}θ}}$．
（1）求A，B两点的极坐标；
（2）设P为曲线C₂上动点，求|PA|²+|PB|²的最大值．

3．已知向量$\overrightarrow{a}$=（1，-2），$\overrightarrow{b}$=（-2，2）则向量$\overrightarrow{a}$在向量$\overrightarrow{b}$方向上的投影为-$\frac{3\sqrt{2}}{2}$．

10．设函数g（x）=$\frac{1+sinx-cosx}{x}$（0＜x≤π），求：
（1）g′（x），（x²g′（x）+1）′；
（2）分别求满足（x²g′（x）+1）′≥0，（x²g′（x）+1）′＜0的x的范围．

20．如果函数y=$\frac{x+1}{x+a}$在（-$\frac{1}{2}$，+∞）上为减函数，求参数a的取值范围．

7．在极坐标系中，已知圆C圆心的极坐标为（$\sqrt{2}$，$\frac{π}{4}$），半径为$\sqrt{3}$．
（1）求圆C的极坐标方程；
（2）以极点为原点，以极轴为x轴正半轴建立直角坐标系，已知直线l的参数方程为$\left\{\begin{array}{l}{x=2+tcosα}\\{y=2+tsinα}\end{array}\right.$（t为参数），直线l交圆C于A、B两点，且|AB|∈[2$\sqrt{2}$，2$\sqrt{3}$），求直线l的斜率k的取值范围．

4．（x²+2）（x-$\frac{1}{x}$）⁶的展开式中常数项为（　　）

5．用计算器求在0°～360°范围内的角x（精确到0.01°）：
（1）cosx=0.12；（2）sinx=0.45．

试题分类