题目内容
 如图,已知鞭形ABEF所在平面与直角梯形ABCD所在平面互相垂直,AB=2AD=2CD=4,∠BAD=∠CDA=90°,∠EFA=60°,点H,G分别是线段EF,BC的中点,点M为HE的中点.
如图,已知鞭形ABEF所在平面与直角梯形ABCD所在平面互相垂直,AB=2AD=2CD=4,∠BAD=∠CDA=90°,∠EFA=60°,点H,G分别是线段EF,BC的中点,点M为HE的中点.(Ⅰ)求证:MG∥平面ADF.
(Ⅱ)求证:平面AHC⊥平面BCE.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:(Ⅰ)取AD的中点N,连接FN,NG,由于G为BC的中点,ABCD为直角梯形,AB=2CD=4,进而可知NG∥AB,且NG=3,又ABEF为菱形,推断出EF∥AB,且EF=AB=4,又H为EF的中点,M为HE的中点,推断出FM=3,且FM∥NG,进而可知四边形FMGN为平行四边形,即MG∥FN,利用线面平行的判定定理知MG∥平面ADF.
(Ⅱ)连接AE,因为ABFE为菱形,∠EFA=60°,H为EF的中点,根据AH⊥EF,即有AH⊥AB,平面ABEF⊥平面ABCD,AB为面ABEF与面ABCD的交线,进而可知AH⊥面ABCD,根据线面垂直的性质可知AH⊥BC,在直角梯形ABCD中,∠BAD=∠CDA=90°,AB=4,CD=AD=2,进而可求得∠ABC,根据AB∥CD,求得∠BCD,又在△ADC中,∠ADC=90°,AD=CD,
求得∠ACD,进而可知∠ACB=∠BCD-∠ACD=90°,即AC⊥BC,根据线面垂直的判定定理知BC⊥平面AHC,最后根据面面垂直的判定定理推断出平面AHC⊥平面BCE.
(Ⅱ)连接AE,因为ABFE为菱形,∠EFA=60°,H为EF的中点,根据AH⊥EF,即有AH⊥AB,平面ABEF⊥平面ABCD,AB为面ABEF与面ABCD的交线,进而可知AH⊥面ABCD,根据线面垂直的性质可知AH⊥BC,在直角梯形ABCD中,∠BAD=∠CDA=90°,AB=4,CD=AD=2,进而可求得∠ABC,根据AB∥CD,求得∠BCD,又在△ADC中,∠ADC=90°,AD=CD,
求得∠ACD,进而可知∠ACB=∠BCD-∠ACD=90°,即AC⊥BC,根据线面垂直的判定定理知BC⊥平面AHC,最后根据面面垂直的判定定理推断出平面AHC⊥平面BCE.
解答:
证明:(Ⅰ)取AD的中点N,连接FN,NG,
∵G为BC的中点,ABCD为直角梯形,AB=2CD=4,
∴NG∥AB,且NG=
=3,
又ABEF为菱形,
∴EF∥AB,且EF=AB=4,
又∵H为EF的中点,M为HE的中点,
∴FM=3,且FM∥NG,
∴四边形FMGN为平行四边形.
∴MG∥FN,
又∵FN?平面ADF,MG?平面ADF,
∴MG∥平面ADF.
(Ⅱ)连接AE,因为ABFE为菱形,∠EFA=60°,H为EF的中点,
∴AH⊥EF,即有AH⊥AB,
∵平面ABEF⊥平面ABCD,AB为面ABEF与面ABCD的交线,
∴AH⊥面ABCD,
∵BC?平面ABCD,
∴AH⊥BC,
∵在直角梯形ABCD中,∠BAD=∠CDA=90°,AB=4,CD=AD=2,
∴∠ABC=45°,
∵AB∥CD,
∴∠BCD=135°
又在△ADC中,∠ADC=90°,AD=CD,
∴∠ACD=45°,
∴∠ACB=∠BCD-∠ACD=90°,即AC⊥BC,
又AH?平面AHC,AC?平面AHC,
∴BC⊥平面AHC,
∵BC?平面BCE,
∴平面AHC⊥平面BCE.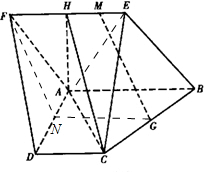
∵G为BC的中点,ABCD为直角梯形,AB=2CD=4,
∴NG∥AB,且NG=
| AB+CD |
| 2 |
又ABEF为菱形,
∴EF∥AB,且EF=AB=4,
又∵H为EF的中点,M为HE的中点,
∴FM=3,且FM∥NG,
∴四边形FMGN为平行四边形.
∴MG∥FN,
又∵FN?平面ADF,MG?平面ADF,
∴MG∥平面ADF.
(Ⅱ)连接AE,因为ABFE为菱形,∠EFA=60°,H为EF的中点,
∴AH⊥EF,即有AH⊥AB,
∵平面ABEF⊥平面ABCD,AB为面ABEF与面ABCD的交线,
∴AH⊥面ABCD,
∵BC?平面ABCD,
∴AH⊥BC,
∵在直角梯形ABCD中,∠BAD=∠CDA=90°,AB=4,CD=AD=2,
∴∠ABC=45°,
∵AB∥CD,
∴∠BCD=135°
又在△ADC中,∠ADC=90°,AD=CD,
∴∠ACD=45°,
∴∠ACB=∠BCD-∠ACD=90°,即AC⊥BC,
又AH?平面AHC,AC?平面AHC,
∴BC⊥平面AHC,
∵BC?平面BCE,
∴平面AHC⊥平面BCE.

点评:本题主要考查了面面垂直的判定定理,线面平行的判定定理及线面垂直的判定定理的应用.考查了学生基础知识的综合运用.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
已知a、b是正常数,a≠b,x、y∈(0,+∞),不等式
+
≥
(*式)恒成立(等号成立的条件是ay=bx),利用(*式)的结果求函数f(x)=
+
(x∈(0,
))的最小值( )
| a2 |
| x |
| b2 |
| y |
| (a+b)2 |
| x+y |
| 2 |
| x |
| 9 |
| 1-2x |
| 1 |
| 2 |
| A、121 | ||
| B、169 | ||
| C、25 | ||
D、11+6
|
若关于x,y的方程x2•sinα-y2•cosα=1所表示的焦点在x轴的双曲线,则方程(x+cosα)2+(y+sinα)2=1所表示的圆的圆心在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
若向量
,
,
两两所成的角相等,且|
|=|
|=|
|=1,则|
+
+
|=( )
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| A、0 | ||
| B、3 | ||
| C、3或 0 | ||
D、1或
|
已知A={x|
>1},B={x||x|<a},若∅?B⊆A,则实数a的取值范围是( )
| 4 |
| x+1 |
| A、a<1 | B、a≤1 |
| C、1≤a≤3 | D、0<a≤1 |
 抛物线y=
抛物线y=