题目内容
已知a、b是正常数,a≠b,x、y∈(0,+∞),不等式
+
≥
(*式)恒成立(等号成立的条件是ay=bx),利用(*式)的结果求函数f(x)=
+
(x∈(0,
))的最小值( )
| a2 |
| x |
| b2 |
| y |
| (a+b)2 |
| x+y |
| 2 |
| x |
| 9 |
| 1-2x |
| 1 |
| 2 |
| A、121 | ||
| B、169 | ||
| C、25 | ||
D、11+6
|
考点:函数的最值及其几何意义,不等式
专题:函数的性质及应用
分析:由题目要求,利用已给的性质求函数f(x)的最小值,类比基本不等式求最值思路,可将函数左边变形后,运用所给规律时,使不等式
+
≥
右边分母为常数即可,为此将f(x)=
+
(x∈(0,
))中的“
”变成“
”,然后套用规律求出f(x)的最小值.
| a2 |
| x |
| b2 |
| y |
| (a+b)2 |
| x+y |
| 2 |
| x |
| 9 |
| 1-2x |
| 1 |
| 2 |
| 2 |
| x |
| 4 |
| 2x |
解答:
解:由已知x∈(0,
),所以x>0,1-2x>0,
又∵不等式
+
≥
(*式)恒成立(等号成立的条件是ay=bx),
∴f(x)=
+
=
+
≥
=25,
当且仅当2(1-2x)=2x•3,即x=
时取等号,显然成立,
∴函数f(x)=
+
(x∈(0,
))的最小值为25.
故选C
| 1 |
| 2 |
又∵不等式
| a2 |
| x |
| b2 |
| y |
| (a+b)2 |
| x+y |
∴f(x)=
| 2 |
| x |
| 9 |
| 1-2x |
| 22 |
| 2x |
| 32 |
| 1-2x |
| (2+3)2 |
| 2x+1-2x |
当且仅当2(1-2x)=2x•3,即x=
| 1 |
| 5 |
∴函数f(x)=
| 2 |
| x |
| 9 |
| 1-2x |
| 1 |
| 2 |
故选C
点评:此题的解法是建立在运用基本不等式求最值的思路基础上的,要使左边取得最小值,只需①a、b是正常数,a≠b,x、y∈(0,+∞);②x+y是常数;③等号成立的条件ay=bx存在.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 把正整数按上小下大、左小右大的原则排成如图三角形数表(每行比上一行多一个数):设ai,j(i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a4,2=8,则a51,25为
把正整数按上小下大、左小右大的原则排成如图三角形数表(每行比上一行多一个数):设ai,j(i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a4,2=8,则a51,25为已知函数f(x)=(
)x-log2x,若实数x0是函数f(x)的零点,且0<x<x0,则函数f(x)的值( )
| 1 |
| 3 |
| A、等于0 | B、恒为正 |
| C、恒为负 | D、不大于0 |
已如f(x)是定义在R上的偶函数,且满足f(x+2)=f(x),当x∈[0,1]时,f(x)=2x.若在区间[-2,3]上方程ax+2a-f(x)=0恰有四个不相等的实数根,则实数a的取值范围 是( )
A、(
| ||||
B、(
| ||||
C、(0,
| ||||
D、(0,
|
已知盒中装有3只螺口与2只卡口灯泡,这些灯泡的外形与功率都相同且灯口向下放着,现需要一只卡口灯泡,电工师傅每次从中任取一只并不放回,则在他第1次抽到的是螺口灯泡的条件下,第2次抽到的是卡口灯泡的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若
与
不共线,实数x、y满足等式2x
+(3-y)
=x
+(3y+1)
,则实数x+y=( )
| a |
| b |
| a |
| b |
| b |
| a |
| A、1 | B、2 | C、3 | D、-2 |
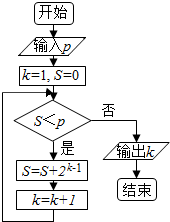
执行如图所示的程序框图,若输出的k=6,则输入的整数p的最大值为( )

| A、7 | B、15 | C、31 | D、63 |
 如图,已知鞭形ABEF所在平面与直角梯形ABCD所在平面互相垂直,AB=2AD=2CD=4,∠BAD=∠CDA=90°,∠EFA=60°,点H,G分别是线段EF,BC的中点,点M为HE的中点.
如图,已知鞭形ABEF所在平面与直角梯形ABCD所在平面互相垂直,AB=2AD=2CD=4,∠BAD=∠CDA=90°,∠EFA=60°,点H,G分别是线段EF,BC的中点,点M为HE的中点.