题目内容
已知f(x)=x3-2x2+x+6,则f(x)在点P(-1,2)处的切线与坐标轴围成的三角形面积等于( )
| A、4 | ||
| B、5 | ||
C、
| ||
D、
|
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:先对函数进行求导,求出在x=1处的导数值即为切线的斜率值,从而写出切线方程,然后求出切线方程与两坐标轴的交点可得三角形面积.
解答:
解:∵f(x)=x3-2x2+x+6,f′(x)=3x2-4x+1,
∴f′(-1)=8,
点P(-1,2)处的切线为:y=8x+10与坐标轴的交点为:(0,10),(-
,0)
S=
×
×10=
,
故选:C.
∴f′(-1)=8,
点P(-1,2)处的切线为:y=8x+10与坐标轴的交点为:(0,10),(-
| 5 |
| 4 |
S=
| 1 |
| 2 |
| 5 |
| 4 |
| 25 |
| 4 |
故选:C.
点评:本题主要考查导数的几何意义,即函数在某点处的导数值等于该点的切线的斜率.属中档题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
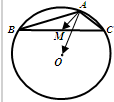 如图,O为△ABC的外心,AB=6,AC=4,∠BAC为钝角,M是边BC的中点,则
如图,O为△ABC的外心,AB=6,AC=4,∠BAC为钝角,M是边BC的中点,则| AM |
| AO |
| A、-10 | B、36 | C、16 | D、13 |
下列函数,是周期函数的为( )
| A、y=sin|x| |
| B、y=cos|x| |
| C、y=tan|x| |
| D、y=(x-1)0 |
 如图,△ABC的重心为G,O是△ABC所在平面上一点,
如图,△ABC的重心为G,O是△ABC所在平面上一点,