题目内容
已知函数f(x)=lnx-kx+1(k∈R).
(Ⅰ)若x轴是曲线f(x)=lnx-kx+1一条切线,求k的值;
(Ⅱ)若f(x)≤0恒成立,试确定实数k的取值范围.
(Ⅰ)若x轴是曲线f(x)=lnx-kx+1一条切线,求k的值;
(Ⅱ)若f(x)≤0恒成立,试确定实数k的取值范围.
考点:利用导数研究曲线上某点切线方程,利用导数求闭区间上函数的最值
专题:综合题,导数的综合应用
分析:(1)函数f(x)的定义域为(0,+∞),f′(x)=
-k=0,可得切点的坐标,进而可求k的值;
(2)确定函数的单调区间,k≤0时,f(x)在(0,+∞)上是增函数,而f(1)=1-k>0,f(x)≤0不成立,故k>0,又由(1)知f(x)的最大值为f(
),由此能确定实数k的取值范围.
| 1 |
| x |
(2)确定函数的单调区间,k≤0时,f(x)在(0,+∞)上是增函数,而f(1)=1-k>0,f(x)≤0不成立,故k>0,又由(1)知f(x)的最大值为f(
| 1 |
| k |
解答:
解:(1)函数f(x)的定义域为(0,+∞),f′(x)=
-k=0,
∴x=
,
由ln
-1+1=0,可得k=1;
(2)当k≤0时,f′(x)=
-k>0,f(x)在(0,+∞)上是增函数;
当k>0时,若x∈(0,
)时,有f′(x)>0,若x∈(
,+∞)时,有f′(x)<0,
则f(x)在(0,
)上是增函数,在(
,+∞)上是减函数.
k≤0时,f(x)在(0,+∞)上是增函数,
而f(1)=1-k>0,f(x)≤0不成立,故k>0,
∵f(x)的最大值为f(
),要使f(x)≤0恒成立,
则f(
)≤0即可,即-lnk≤0,得k≥1.
| 1 |
| x |
∴x=
| 1 |
| k |
由ln
| 1 |
| k |
(2)当k≤0时,f′(x)=
| 1 |
| x |
当k>0时,若x∈(0,
| 1 |
| k |
| 1 |
| k |
则f(x)在(0,
| 1 |
| k |
| 1 |
| k |
k≤0时,f(x)在(0,+∞)上是增函数,
而f(1)=1-k>0,f(x)≤0不成立,故k>0,
∵f(x)的最大值为f(
| 1 |
| k |
则f(
| 1 |
| k |
点评:本题考查导数的几何意义,考查函数单调区间的求法,确定实数的取值范围,渗透了分类与整合的数学思想,培养学生的抽象概括能力、推理论证能力、运算求解能力和创新意识.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
已知f(x)=x3-2x2+x+6,则f(x)在点P(-1,2)处的切线与坐标轴围成的三角形面积等于( )
| A、4 | ||
| B、5 | ||
C、
| ||
D、
|
己知命题p:“a>b”是“2a>2b”的充要条件;q:?x∈R,|x+l|≤x,则( )
| A、¬p∨q为真命题 |
| B、p∧¬q为假命题 |
| C、p∧q为真命题 |
| D、p∨q为真命题 |
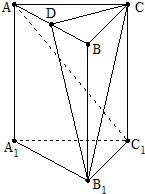 如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1,AC⊥BC,点D是AB的中点.
如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1,AC⊥BC,点D是AB的中点.