题目内容
求函数f(x)=x2-2x-3,x∈[0,b]的值域.
考点:二次函数的性质
专题:函数的性质及应用
分析:通过讨论b的范围结合二次函数的性质从而得到函数的值域.
解答:
解:函数f(x)=x2-2x-3=(x-1)2-4,
当b≤1时,函数f(x)在[0,b]递减,
∴f(x)max=f(0)=-3,f(x)min=f(b)=b2-2b-3,
当1<b≤2时,函数f(x)在[0,1)递减,在(1,b]递增,
∴f(x)max=f(0)=-3,f(x)min=f(1)=-4,
当b>2时,函数f(x)在[0,1)递减,在(1,b]递增,
∴f(x)max=f(b)=b2-2b-3,f(x)min=f(1)=-4.
当b≤1时,函数f(x)在[0,b]递减,
∴f(x)max=f(0)=-3,f(x)min=f(b)=b2-2b-3,
当1<b≤2时,函数f(x)在[0,1)递减,在(1,b]递增,
∴f(x)max=f(0)=-3,f(x)min=f(1)=-4,
当b>2时,函数f(x)在[0,1)递减,在(1,b]递增,
∴f(x)max=f(b)=b2-2b-3,f(x)min=f(1)=-4.
点评:本题考查了二次函数的性质,考查了分类讨论思想,是一道基础题.

练习册系列答案
相关题目
已知f(x)=x3-2x2+x+6,则f(x)在点P(-1,2)处的切线与坐标轴围成的三角形面积等于( )
| A、4 | ||
| B、5 | ||
C、
| ||
D、
|
 如图,椭圆E:
如图,椭圆E: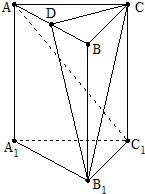 如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1,AC⊥BC,点D是AB的中点.
如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1,AC⊥BC,点D是AB的中点.