题目内容
已知正实数a,b满足:(a-1)(b-1)=4,则ab的最小值是 .
考点:基本不等式
专题:不等式的解法及应用
分析:把(a-1)(b-1)=4,化为ab=a+b+3.由于a>0,b>0,利用基本不等式可得ab≥2
+3,解出即可.
| ab |
解答:
解:∵(a-1)(b-1)=4,∴ab=a+b+3.
∴a>0,b>0,∴ab≥2
+3,当且仅当a=b=3时取等号.
化为(
-3)(
+1)≥0,∴
-3≥0,解得ab≥9.
∴ab的最小值是9.
故答案为:9.
∴a>0,b>0,∴ab≥2
| ab |
化为(
| ab |
| ab |
| ab |
∴ab的最小值是9.
故答案为:9.
点评:本题考查了基本不等式的性质,属于基础题.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
设f(x)是周期为2的奇函数,当0≤x≤1时,f(x)=4x(1-x),则f(-
)=( )
| 9 |
| 2 |
| A、1 | B、-1 | C、-63 | D、63 |
直线(a-1)x+y-a-3=0(a>1),当此直线在x,y轴的截距和最小时,实数a的值是( )
| A、1 | ||
B、
| ||
| C、2 | ||
| D、3 |
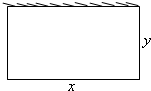 现要用一段长为l的篱笆围成一边靠墙的矩形菜园(如图所示),则围成的菜园最大面积是
现要用一段长为l的篱笆围成一边靠墙的矩形菜园(如图所示),则围成的菜园最大面积是