题目内容
已知椭圆
+
=1的一个焦点为F(2,0),且离心率为
.
(Ⅰ)求椭圆方程;
(Ⅱ)过点M(3,0)且斜率为k的直线与椭圆交于A,B两点,点A关于x轴的对称点为C,求△MBC面积的最大值.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
(Ⅰ)求椭圆方程;
(Ⅱ)过点M(3,0)且斜率为k的直线与椭圆交于A,B两点,点A关于x轴的对称点为C,求△MBC面积的最大值.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由题意知c=2,
=
,a2=b2+c2,由此能求出椭圆方程.
(Ⅱ)直线l的方程为y=k(x-3).联立方程组
,得(3k2+1)x2-18k2x+27k2-6=0.由韦达定理结合已知条件推导出S△MBC=|S△ABC-S△AMC|=|y1|(3-x2)=|k|(3-x1)(3-x2)≤
,由此能求出△MBC面积S的最大值.
| c |
| a |
| ||
| 3 |
(Ⅱ)直线l的方程为y=k(x-3).联立方程组
|
| ||
| 2 |
解答:
解:(Ⅰ)∵椭圆
+
=1的一个焦点为F(2,0),且离心率为
.
∴c=2,
=
,a2=b2+c2,
解得a2=6,b2=2.
故椭圆方程为
+
=1.
(Ⅱ)直线l的方程为y=k(x-3).
联立方程组
,消去y并整理,
得(3k2+1)x2-18k2x+27k2-6=0. (*)
设A(x1,y1),B(x2,y2).
故x1+x2=
,x1x2=
.
不妨设x1<x2,显然x1,x2均小于3.
则S△AMC=
•|2y1|•(3-x1)=|y1|(3-x1),
S△ABC=
•|2y1|•(x2-x1)=|y1|(x2-x1).
S△MBC=|S△ABC-S△AMC|=|y1|(3-x2)=|k|(3-x1)(3-x2)
=|k|[9-3(x1+x2)+x1x2]=
≤
=
.
等号成立时,解得k2=
,此时方程(*)为 2x2-6x+3=0,满足△>0.
所以△MBC面积S的最大值为
.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
∴c=2,
| c |
| a |
| ||
| 3 |
解得a2=6,b2=2.
故椭圆方程为
| x2 |
| 6 |
| y2 |
| 2 |
(Ⅱ)直线l的方程为y=k(x-3).
联立方程组
|
得(3k2+1)x2-18k2x+27k2-6=0. (*)
设A(x1,y1),B(x2,y2).
故x1+x2=
| 18k2 |
| 3k2+1 |
| 27k2-6 |
| 3k2+1 |
不妨设x1<x2,显然x1,x2均小于3.
则S△AMC=
| 1 |
| 2 |
S△ABC=
| 1 |
| 2 |
S△MBC=|S△ABC-S△AMC|=|y1|(3-x2)=|k|(3-x1)(3-x2)
=|k|[9-3(x1+x2)+x1x2]=
| 3|k| |
| 3k2+1 |
| 3|k| | ||
2
|
| ||
| 2 |
等号成立时,解得k2=
| 1 |
| 3 |
所以△MBC面积S的最大值为
| ||
| 2 |
点评:本题考查椭圆方程的求法,考查三角形面积的最大值的求法,解题时要认真审题,注意均值定理的合理运用.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 如图,已知正方形ABCD的边长为6,点E,F分别在边AB,AD上,AE=AF=4,现将△AEF沿线段EF折起到△A′EF位置,使得A′C=2
如图,已知正方形ABCD的边长为6,点E,F分别在边AB,AD上,AE=AF=4,现将△AEF沿线段EF折起到△A′EF位置,使得A′C=2 如图,已知AB是圆柱OO1底面圆O的直径,底面半径R=1,圆柱的表面积为8π;点C在底面圆O上,且直线A1C与下底面所成的角的大小为60°.
如图,已知AB是圆柱OO1底面圆O的直径,底面半径R=1,圆柱的表面积为8π;点C在底面圆O上,且直线A1C与下底面所成的角的大小为60°.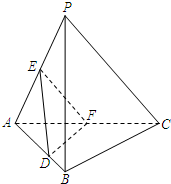 如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,∠BAC=60°,E,F分别是AP,AC的中点,点D在棱AB上,且AD=AC.求证:
如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,∠BAC=60°,E,F分别是AP,AC的中点,点D在棱AB上,且AD=AC.求证: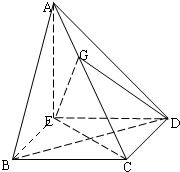 如图,在四棱锥A-BCDE中,AE⊥平面BCDE,∠ABC=∠BCD=∠CDA=90°,AC=6
如图,在四棱锥A-BCDE中,AE⊥平面BCDE,∠ABC=∠BCD=∠CDA=90°,AC=6