题目内容
已知椭圆T:
+
=1(a>b>0).
(Ⅰ)若椭圆T的离心率为
,过焦点且垂直于z轴的直线被椭圆截得弦长为
.
①求椭圆方程;
②过点P(2,1)的两条直线分别与椭圆F交于点A,C和B,D,若AB∥CD,求直线AB的斜率;
(Ⅱ)设P(x0,y0)为椭圆T内一定点(不在坐标轴上),过点P的两条直线分别与椭圆T交于点A,C和B,D,且AB∥CD,类比(Ⅰ)②直接写出直线T的斜率.(不必证明)
| ||
|
| ||
|
(Ⅰ)若椭圆T的离心率为
| ||
| 3 |
| 8 |
| 3 |
①求椭圆方程;
②过点P(2,1)的两条直线分别与椭圆F交于点A,C和B,D,若AB∥CD,求直线AB的斜率;
(Ⅱ)设P(x0,y0)为椭圆T内一定点(不在坐标轴上),过点P的两条直线分别与椭圆T交于点A,C和B,D,且AB∥CD,类比(Ⅰ)②直接写出直线T的斜率.(不必证明)
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)①由已知条件稚导出
,由此能求出椭圆Г的方程.
②设点A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),
=λ
.则2-x1=λ(x3-2),1-y1=λ(y3-1),故x3=
,y3=
,由此入手能求出直线AB的斜率.
(Ⅱ)归纳总结(Ⅰ)②的规律,类比(Ⅰ)②能够直接写出直线T的斜率.
|
②设点A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),
| AP |
| PC |
| 2(1+λ)-x1 |
| λ |
| (1+λ)-y1 |
| λ |
(Ⅱ)归纳总结(Ⅰ)②的规律,类比(Ⅰ)②能够直接写出直线T的斜率.
解答:
解:(Ⅰ)①∵椭圆T:
+
=1(a>b>0),
椭圆T的离心率为
,过焦点且垂直于z轴的直线被椭圆截得弦长为
,
∴
,解得
,…(2分)
∴椭圆Г的方程为
+
=1.…(3分)
②设点A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),
=λ
.
则2-x1=λ(x3-2),1-y1=λ(y3-1),
故x3=
,y3=
.…(5分)
∵点C在椭圆上,∴
+
=1,
则
+
=1
整理得 (1+λ)2(
+
)-2(1+λ)(
+
)+
+
=λ2…(6分)
由点A在椭圆上知
+
=1,
故(1+λ)2(
+
)-2(1+λ)(
+
)=λ2-1.①…(7分)
又AB∥CD,则
=λ
.
同理可得 (1+λ)2(
+
)-2(1+λ)(
+
)=λ2-1.②…(8分)
①-②得
(x2-x1)+
(y2-y1)=0.
由题意可知x1≠x2,则直线AB的斜率为k=
=-
.…(10分)
(Ⅱ)直线AB的斜率为-
.…(13分)
| ||
|
| ||
|
椭圆T的离心率为
| ||
| 3 |
| 8 |
| 3 |
∴
|
|
∴椭圆Г的方程为
| x2 |
| 9 |
| y2 |
| 4 |
②设点A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),
| AP |
| PC |
则2-x1=λ(x3-2),1-y1=λ(y3-1),
故x3=
| 2(1+λ)-x1 |
| λ |
| (1+λ)-y1 |
| λ |
∵点C在椭圆上,∴
| ||
| 9 |
| ||
| 4 |
则
| [2(1+λ)-x1]2 |
| 9λ2 |
| [(1+λ)-y1]2 |
| 4λ2 |
整理得 (1+λ)2(
| 4 |
| 9 |
| 1 |
| 4 |
| 2x1 |
| 9 |
| y1 |
| 4 |
| ||
| 9 |
| ||
| 4 |
由点A在椭圆上知
| ||
| 9 |
| ||
| 4 |
故(1+λ)2(
| 4 |
| 9 |
| 1 |
| 4 |
| 2x1 |
| 9 |
| y1 |
| 4 |
又AB∥CD,则
| BP |
| PD |
同理可得 (1+λ)2(
| 4 |
| 9 |
| 1 |
| 4 |
| 2x2 |
| 9 |
| y2 |
| 4 |
①-②得
| 2 |
| 9 |
| 1 |
| 4 |
由题意可知x1≠x2,则直线AB的斜率为k=
| y2-y1 |
| x2-x1 |
| 8 |
| 9 |
(Ⅱ)直线AB的斜率为-
| b2x0 |
| a2y0 |
点评:本题考查椭圆标准方程,简单几何性质,直线与椭圆的位置关系等基础知识.考查运算求解能力,推理论证能力,解题时要认真审题,注意椭圆简单性质的灵活运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图所示,有三根针和套在一根针上若干金属片.按下列规则,把金属片从一根针上全部移到另一根针上.
如图所示,有三根针和套在一根针上若干金属片.按下列规则,把金属片从一根针上全部移到另一根针上. 如图,已知AB是圆柱OO1底面圆O的直径,底面半径R=1,圆柱的表面积为8π;点C在底面圆O上,且直线A1C与下底面所成的角的大小为60°.
如图,已知AB是圆柱OO1底面圆O的直径,底面半径R=1,圆柱的表面积为8π;点C在底面圆O上,且直线A1C与下底面所成的角的大小为60°.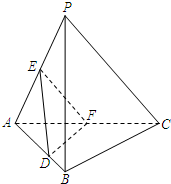 如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,∠BAC=60°,E,F分别是AP,AC的中点,点D在棱AB上,且AD=AC.求证:
如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,∠BAC=60°,E,F分别是AP,AC的中点,点D在棱AB上,且AD=AC.求证: