题目内容
16.已知函数f(x)=x3+x2-x+1,则此函数在[-2,$\frac{1}{2}$]上的最大值等于2.分析 对函数f(x)求导,利用导数研究函数在区间[-2,$\frac{1}{2}$]上的单调性,根据函数的变化规律,确定函数在区间上最大值的位置,求值即可.
解答 解:由题意函数f(x)=x3+x2-x+1,可得y′=3x2+2x-1
令y′>0,解得x>$\frac{1}{3}$或x<-1
故函数f(x)在(-2,-1)单调递减,在(-1,$\frac{1}{3}$)上单调递减,在($\frac{1}{3}$,$\frac{1}{2}$)上单调增
因为f($\frac{1}{2}$)=$\frac{7}{8}$,f(-1)=2,
故函数f(x)=x3+x2-x+1,在[-2,$\frac{1}{2}$]上的最大值等于2.
故答案为:2.
点评 本题考查用导数判断函数的单调性,利用单调性求函数的最值,利用单调性研究函数的最值,是基础题.

练习册系列答案
相关题目
6.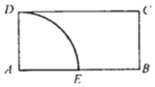 如图,在矩形ABCD中,AD=1,AB=2,以A为圆心,AD为半径在矩形内部作扇形AED,若向矩形ABCD内部随机投放一点,则所投点落在扇形外部的概率为( )
如图,在矩形ABCD中,AD=1,AB=2,以A为圆心,AD为半径在矩形内部作扇形AED,若向矩形ABCD内部随机投放一点,则所投点落在扇形外部的概率为( )
 如图,在矩形ABCD中,AD=1,AB=2,以A为圆心,AD为半径在矩形内部作扇形AED,若向矩形ABCD内部随机投放一点,则所投点落在扇形外部的概率为( )
如图,在矩形ABCD中,AD=1,AB=2,以A为圆心,AD为半径在矩形内部作扇形AED,若向矩形ABCD内部随机投放一点,则所投点落在扇形外部的概率为( )| A. | $\frac{π}{8}$ | B. | 1-$\frac{π}{8}$ | C. | $\frac{π}{4}$ | D. | 1-$\frac{π}{4}$ |
7.直线l1:(m-1)x+y=4m-1与直线l2:2x-3y=5互相平行的充要条件是( )
| A. | m=$\frac{2}{3}$ | B. | m=$\frac{1}{3}$ | C. | m=-$\frac{2}{3}$ | D. | m=-$\frac{1}{3}$ |
11.利用计算机产生0~1之间的均匀随机数a,则事件“3a-1<0”发生的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
10.已知p:(x-2)(x+1)>0;q:|x|<a,若¬p是q的必要不充分条件,则a的取值范围是( )
| A. | a<1 | B. | a≤1 | C. | a<2 | D. | a≤2 |
8.设 f(x)是定义在[a-1,2]上偶函数,则f(x)=ax2+bx+1在[-2,0]上是( )
| A. | 增函数 | B. | 减函数 | ||
| C. | 先增后减函数 | D. | 与a,b有关,不能确定 |