题目内容
1．已知复数Z=$\frac{1}{1+i}+{i^3}$（i为虚数单位），则复数Z的模为（ ）| A． | 2 | B． | $\frac{10}{4}$ | C． | $\frac{{\sqrt{10}}}{2}$ | D． | -1 |
分析 利用复数代数形式的乘除运算化简，再由复数模的计算公式得答案．
解答 解：∵Z=$\frac{1}{1+i}+{i^3}$=$\frac{1-i}{（1+i）（1-i）}-i=\frac{1}{2}-\frac{3}{2}i$．
∴$|Z|=\sqrt{（\frac{1}{2}）^{2}+（-\frac{3}{2}）^{2}}=\frac{\sqrt{10}}{2}$．
故选：C．
点评 本题考查复数代数形式的乘除运算，考查了复数模的求法，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
11．几个月前，成都街头开始兴起“mobike”、“ofo”等共享单车，这样的共享单车为很多市民解决了最后一公里的出行难题，然而，这种模式也遇到了一些让人尴尬的问题，比如乱停乱放，或将共享单车占为“私有”等．
为此，某机构就是否支持发展共享单车随机调查了50人，他们年龄的分布及支持发展共享单车的人数统计如表：
（1）由以上统计数据填写下面的2×2列联表，并判断能否在犯错误的概率不超过0.1的前提下，认为年龄与是否支持发展共享单车有关系；
（2）若对年龄在[15，20）[20，25）的被调查人中随机选取两人进行调查，记选中的4人中支持发展共享单车的人数为X，求随机变量X的分布列及数学期望．
参考数据：
参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d．
为此，某机构就是否支持发展共享单车随机调查了50人，他们年龄的分布及支持发展共享单车的人数统计如表：
| 年龄 | [15，20） | [20，25） | [25，30） | [30，35） | [35，40） | [40，45） |
| 受访人数 | 5 | 6 | 15 | 9 | 10 | 5 |
| 支持发展 共享单车人数 | 4 | 5 | 12 | 9 | 7 | 3 |
| 年龄低于35岁 | 年龄不低于35岁 | 合计 | |
| 支持 | |||
| 不支持 | |||
| 合计 |
参考数据：
| P（K2≥k） | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
9．
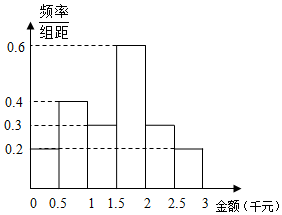某网络营销部门为了统计某市网友2016年12月12日的网购情况，从该市当天参与网购的顾客中随机抽查了男女各30人，统计其网购金额，得到如下频率分布直方图：
若网购金额超过2千元的顾客称为“网购达人”，网购金额不超过2千元的顾客称为“非网购达人”．
（ I）根据频率分布直方图估计网友购物金额的平均值；
（ II）若抽取的“网购达人”中女性占12人，请根据条件完成上面的2×2列联表，并判断是否有99%的把握认为“网购达人”与性别有关？
（参考公式：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d）
某网络营销部门为了统计某市网友2016年12月12日的网购情况，从该市当天参与网购的顾客中随机抽查了男女各30人，统计其网购金额，得到如下频率分布直方图：| 网购达人 | 非网购达人 | 合计 | |
| 男性 | 30 | ||
| 女性 | 12 | 30 | |
| 合计 | 60 |
（ I）根据频率分布直方图估计网友购物金额的平均值；
（ II）若抽取的“网购达人”中女性占12人，请根据条件完成上面的2×2列联表，并判断是否有99%的把握认为“网购达人”与性别有关？
（参考公式：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d）
| P（K2≥k） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
16．设点M（x，y）满足不等式组$\left\{\begin{array}{l}3x-y-6≤0\\ x-y+2≥0\\ x≥0，y≥0\end{array}\right.$，点P（-4a，a）（a＞0），则当$\overrightarrow{OP}•\overrightarrow{OM}$最大时，点M为（ ）
| A． | （0，2） | B． | （0，0） | C． | （4，6） | D． | （2，6） |
6．执行如图所示的程序框图，若输入t的值为5，则输出的S的值为（ ）
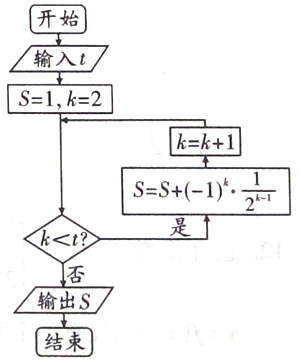
| A． | $\frac{11}{8}$ | B． | $\frac{9}{16}$ | C． | $\frac{5}{4}$ | D． | $\frac{21}{16}$ |
10．在△ABC中，点M为边BC上任意一点，点N为AM的中点，若$\overrightarrow{AN}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$（λ，μ∈R），则λ+μ的值为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{5}$ |
11．已知集合A={x|1＜x＜3}，B={x|y=log2（2-x）}，则A∩B=（ ）
| A． | （0，3） | B． | （0，1） | C． | （1，2） | D． | （2，3） |