题目内容
7.函数f(x)=x2-2x-3在[0,3)上的值域为[-4,0).分析 先对函数式配方f(x)=(x-1)2-4,再根据二次函数的图象和性质得出f(x)的值域.
解答 解:f(x)=(x-1)2-4,
该函数的图象为抛物线,开口向上,
且图象关于直线x=1轴对称,
当x∈[0,3)时,
f(x)min=f(1)=-4,
f(x)max=f(3)=0,(由于x<3,故此处不取“=”),
所以,函数的值域为:[-4,0),
故答案为:[-4,0).
点评 本题主要考查了函数值域的解法,涉及二次函数的图象和性质,考查了配方法与数形结合的解题思想,属于基础题.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
15.已知双曲线的焦距为2$\sqrt{3}$,焦点到一条渐近线的距离为$\sqrt{2}$,则双曲线的标准方程为( )
| A. | x2-$\frac{{y}^{2}}{2}$=1 | B. | $\frac{{x}^{2}}{2}$-y2=1 | ||
| C. | x2-$\frac{{y}^{2}}{2}$=1或y2-$\frac{{x}^{2}}{2}$=1 | D. | $\frac{{x}^{2}}{2}$-y2=1或$\frac{{y}^{2}}{2}$-x2=1 |
17.下列命题中,错误的是( )
| A. | 一条直线与两个平行平面中的一个相交,则必与另一个相交 | |
| B. | 平行于同一个平面的两个平面平行 | |
| C. | 一个平面与两个平行平面相交,交线平行 | |
| D. | 平行于同一条直线的两个平面平行 |
 某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50],[50,60],…,[80,90],[90,100]
某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50],[50,60],…,[80,90],[90,100]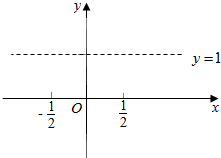 已知直线y=1与曲线y=x2-|x|+a有四个交点.
已知直线y=1与曲线y=x2-|x|+a有四个交点.