题目内容
(理)数列{an}满足a1=1,a2=2,an+1=(1+cos2
)an+sin2
,n=1,2,3….
(1)求a3,a4,并求数列{an}的通项公式;
(2)设bn=
,Sn=b1+b2+…bn.证明:n≥6时,|Sn-2|<
.
| nπ |
| 2 |
| nπ |
| 2 |
(1)求a3,a4,并求数列{an}的通项公式;
(2)设bn=
| a2n-1 | ||
|
| 1 |
| n |
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)由已知结合递推式求出a3,a4,得到数列{a2k-1}是首项为1,公差为1的等差数列,数列{a2k}是首项为2,公比为2的等比数列,在数列的通项公式可求;
(2)把数列{an}的通项公式代入bn=
,利用错位相减法求和,然后利用放缩法证明数列不等式.
(2)把数列{an}的通项公式代入bn=
| a2n-1 | ||
|
解答:
解:(1)∵a1=1,a2=2,
∴a3=(1+cos2
)a1+sin2
=a1+1=2,a4=(1+cos2π)a2+sin2π=2a2=4.
一般地,当n=2k-1(k∈N*)时,a2k+1=[1+cos2
π]a2k-1+sin2
π=a2k-1+1,
即a2k+1-a2k-1=1.
∴数列{a2k-1}是首项为1,公差为1的等差数列,因此a2k-1=k;
当n=2k(k∈N*)时,a2k+2=(1+cos2
)a2k+sin2
=2a2k,
∴数列{a2k}是首项为2,公比为2的等比数列,因此a2k=2k.
故数列{an}的通项公式为an=
;
(2)由(1)知,bn=
=
,
Sn=
+
+
+…+
①
Sn=
+
+
+…+
②
①-②得,
Sn=
+
+…+
-
=1-
-
.
∴Sn=2-
-
=2-
.
要证明n≥6时,|Sn-2|<
.
只需证明当n≥6时,
<1.
令cn=
(n≥6),
则cn+1-cn=
-
=
<0.
∴当n≥6时,cn+1<cn,
因此,当n≥6时,cn≤c6=
=
<1.
于是,当n≥6时,
<1.
综上所述,n≥6时,|Sn-2|<
.
∴a3=(1+cos2
| π |
| 2 |
| π |
| 2 |
一般地,当n=2k-1(k∈N*)时,a2k+1=[1+cos2
| 2k-1 |
| 2 |
| 2k-1 |
| 2 |
即a2k+1-a2k-1=1.
∴数列{a2k-1}是首项为1,公差为1的等差数列,因此a2k-1=k;
当n=2k(k∈N*)时,a2k+2=(1+cos2
| 2kπ |
| 2 |
| 2kπ |
| 2 |
∴数列{a2k}是首项为2,公比为2的等比数列,因此a2k=2k.
故数列{an}的通项公式为an=
|
(2)由(1)知,bn=
| a2n-1 | ||
|
| n |
| 2n |
Sn=
| 1 |
| 2 |
| 2 |
| 22 |
| 3 |
| 23 |
| n |
| 2n |
| 1 |
| 2 |
| 1 |
| 22 |
| 2 |
| 23 |
| 3 |
| 24 |
| n |
| 2n+1 |
①-②得,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n |
| n |
| 2n+1 |
| 1 |
| 2n |
| n |
| 2n+1 |
∴Sn=2-
| 1 |
| 2n-1 |
| n |
| 2n |
| n+2 |
| 2n |
要证明n≥6时,|Sn-2|<
| 1 |
| n |
只需证明当n≥6时,
| n(n+2) |
| 2n |
令cn=
| n(n+2) |
| 2n |
则cn+1-cn=
| (n+1)(n+3) |
| 2n+1 |
| n(n+2) |
| 2n |
| 3-n2 |
| 2n+1 |
∴当n≥6时,cn+1<cn,
因此,当n≥6时,cn≤c6=
| 6×8 |
| 64 |
| 3 |
| 4 |
于是,当n≥6时,
| n(n+2) |
| 2n |
综上所述,n≥6时,|Sn-2|<
| 1 |
| n |
点评:本题考查了数列递推式,考查了错位相减法求数列的和,训练了作差法证明数列不等式,考查了学生的逻辑思维能力,是压轴题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若直线ax+by+c=0过二、三、四象限,则成立的是( )
| A、ab>0,ac>0 |
| B、ab>0,ac<0 |
| C、ab<0,ac>0 |
| D、ab<0,ac<0 |
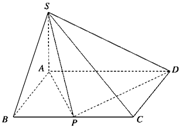 如图,四棱锥S-ABCD的底面是矩形,SA⊥底面ABCD,P为BC边的中点,AD=2,SA=AB=1.则PD与平面SAP所成的角的大小为
如图,四棱锥S-ABCD的底面是矩形,SA⊥底面ABCD,P为BC边的中点,AD=2,SA=AB=1.则PD与平面SAP所成的角的大小为