题目内容
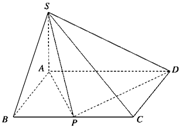如图，四棱锥S-ABCD的底面是矩形，SA⊥底面ABCD，P为BC边的中点，AD=2，SA=AB=1．则PD与平面SAP所成的角的大小为考点：直线与平面所成的角
专题：计算题,空间角
分析：证明PD⊥平面SAP，即可求得PD与平面SAP所成的角的大小．
解答：
解：∵SA⊥平面ABCD，PD?平面ABCD，∴SA⊥PD，
在矩形ABCD中，AD=2，AB=1，P为BC中点，
∴AP⊥PD，
∵SA∩AP=A，∴PD⊥平面SAP．
故PD与平面SAP所成的角的大小为90°．
故答案为：90°．
在矩形ABCD中，AD=2，AB=1，P为BC中点，
∴AP⊥PD，
∵SA∩AP=A，∴PD⊥平面SAP．
故PD与平面SAP所成的角的大小为90°．
故答案为：90°．
点评：本题考查直线与平面所成的角的大小，考查定理的应用，空间想象能力，计算能力．
练习册系列答案
相关题目
对任意向量
，
，下列命题不正确的是（ ）
| a |
| b |
A、|
| ||||||||
B、|
| ||||||||
C、|（λ
| ||||||||
D、|λ
|