题目内容
已知半径为10的圆O中,弦AB的长为10.弦AB所对的圆心角α= rad,α所在的扇形的弧长l= ,α所在的扇形的面积S= .
考点:扇形面积公式
专题:计算题,三角函数的求值
分析:利用圆的性质,可得弦AB所对的圆心角,利用扇形的弧长、面积公式可得结论.
解答:
解:如图,连接OA、OB,则
∵OA=OB=AB=10,
∴△OAB是等边三角形;
∴∠AOB=
,
∴扇形的弧长l=10×
=
扇形的面积S=
lr=
×
×10=
故答案为:
,
,

∵OA=OB=AB=10,
∴△OAB是等边三角形;
∴∠AOB=
| π |
| 3 |
∴扇形的弧长l=10×
| π |
| 3 |
| 10π |
| 3 |
扇形的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 10π |
| 3 |
| 50π |
| 3 |
故答案为:
| π |
| 3 |
| 10π |
| 3 |
| 50π |
| 3 |
点评:本题考查扇形的弧长、面积公式,考查学生的计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若ax2+4ax+3≥0恒成立,a的取值范围是( )
A、(0,
| ||
B、(0,
| ||
C、[0,
| ||
D、[0,
|
集合A={x∈R|0<x≤2},B={x∈R|x2-x-2>0},则A∩(CRB)=( )
| A、(-1,2) |
| B、[-1,2] |
| C、(0,2) |
| D、(0,2] |
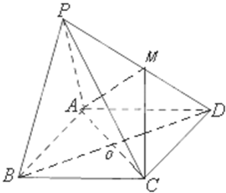 如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知
如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知