题目内容
17.已知函数f(x)=|x+2|-2|x-1|.(Ⅰ)求不等式f(x)≥-2的解集M;
(Ⅱ)对任意x∈[a,+∞],都有f(x)≤x-a成立,求实数a的取值范围.
分析 (Ⅰ)通过对x≤-2,-2<x<1与x≥1三类讨论,去掉绝对值符号,解相应的一次不等式,最后取其并集即可;
(Ⅱ)在坐标系中,作出f(x)=$\left\{\begin{array}{l}{x-4,x≤-2}\\{3x,-2<x<1}\\{4-x,x≥1}\end{array}\right.$的图象,对任意x∈[a,+∞),都有f(x)≤x-a成立,分-a≥2与-a<2讨论,即可求得实数a的取值范围.
解答 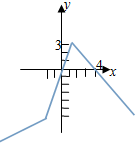 解:(Ⅰ)∵函数f(x)=|x+2|-2|x-1|,∴不等式f(x)≥-2即 $\left\{\begin{array}{l}{x≤-2}\\{x-4≥-2}\end{array}\right.$①,或$\left\{\begin{array}{l}{-2<x<1}\\{3x≥-2}\end{array}\right.$ ②,或 $\left\{\begin{array}{l}{x≥1}\\{4-x≥-2}\end{array}\right.$③.
解:(Ⅰ)∵函数f(x)=|x+2|-2|x-1|,∴不等式f(x)≥-2即 $\left\{\begin{array}{l}{x≤-2}\\{x-4≥-2}\end{array}\right.$①,或$\left\{\begin{array}{l}{-2<x<1}\\{3x≥-2}\end{array}\right.$ ②,或 $\left\{\begin{array}{l}{x≥1}\\{4-x≥-2}\end{array}\right.$③.
解①求得x∈∅,解②求得-$\frac{2}{3}$≤x<1,解③求得1≤x≤6,
综上,不等式的解集为M={x|-$\frac{2}{3}$≤x≤6}.
(Ⅱ)对任意x∈[a,+∞],都有f(x)≤x-a成立,函数f(x)=$\left\{\begin{array}{l}{x-4,x≤-2}\\{3x,-2<x<1}\\{4-x,x≥1}\end{array}\right.$ 的图象如图所示:
令y=x-a,则此直线斜率为1,-a表示直线的纵截距,故函数f(x)的图象在直线y=x-a的下方或在直线上.
当直线过(1,3)点时,-a=2,即a=-2;
∴当-a≥2,即a≤-2时,条件成立;
当-a<2,即a>-2时,令-x+4=x-a,得x=2+$\frac{a}{2}$,
∴a≥2+$\frac{a}{2}$,即a≥4时,条件成立,
综上a≤-2或a≥4.
点评 本题考查绝对值不等式的解法,考查分段函数的性质及应用,考查等价转化思想与作图分析能力,突出恒成立问题的考查,属于难题.

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案| A. | $(\sqrt{2},2\sqrt{2}]$ | B. | $(\sqrt{2},2\sqrt{2})$ | C. | $[\sqrt{2},2\sqrt{2})$ | D. | $[\sqrt{2},2\sqrt{2}]$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| 未过度使用 | 过度使用 | 合计 | |
| 未患颈椎病 | 15 | 5 | 20 |
| 患颈椎病 | 10 | 20 | 30 |
| 合计 | 25 | 25 | 50 |
(2)已知在患有颈锥病的10名未过度使用电子产品的大学生中,有3名大学生又患有肠胃炎,现在从上述的10名大学生中,抽取3名大学生进行其他方面的排查,记选出患肠胃炎的学生人数为ε,求ε的分布列及数学期望.
参考数据与公式:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |