题目内容
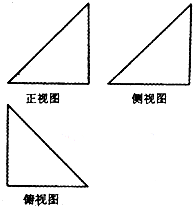 如图,某几何体的三视图均为腰长为1的等腰直角三角形,则此几何体最长的棱长为
如图,某几何体的三视图均为腰长为1的等腰直角三角形,则此几何体最长的棱长为考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:根据三视图得出某几何体的三视图均为腰长为1的等腰直角三角形,可判断三棱锥为P=ABC,Rt△ABC,PC=AB=BC=1,AB⊥BC,PC⊥面ABC,
根据几何体的性质得出PA最长,运用直角三角形判断即可.
根据几何体的性质得出PA最长,运用直角三角形判断即可.
解答:
 解:某几何体的三视图均为腰长为1的等腰直角三角形,可判断三棱锥为P=ABC,Rt△ABC,PC=AB=BC=1,AB⊥BC,PC⊥面ABC,
解:某几何体的三视图均为腰长为1的等腰直角三角形,可判断三棱锥为P=ABC,Rt△ABC,PC=AB=BC=1,AB⊥BC,PC⊥面ABC,
∴根据几何体的性质得出PA最长,
∴AC=
,PC=
=
,
故答案:
,
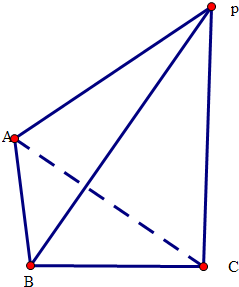
 解:某几何体的三视图均为腰长为1的等腰直角三角形,可判断三棱锥为P=ABC,Rt△ABC,PC=AB=BC=1,AB⊥BC,PC⊥面ABC,
解:某几何体的三视图均为腰长为1的等腰直角三角形,可判断三棱锥为P=ABC,Rt△ABC,PC=AB=BC=1,AB⊥BC,PC⊥面ABC,∴根据几何体的性质得出PA最长,
∴AC=
| 2 |
| 12+2 |
| 3 |
故答案:
| 3 |

点评:本题考查了由三视图运用,关键是对几何体正确还原,并根据三视图的长度求出几何体的几何元素的长度,考查了空间想象能力.

练习册系列答案
相关题目
已知(2x+y-3)+(x+3y-4)λ=0,则x+y的值为( )
| A、0 | B、1 | C、2 | D、3 |
已知α∈(0,π),且sinα+cosα=
,则sinα-cosα的值为( )
| ||
| 2 |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
为了得到函数y=cos(x+
),x∈R,只需把函数y=cosx上所有的点( )
| 1 |
| 4 |
A、向左平行移动
| ||
B、向右平行移动
| ||
C、向左平行移动
| ||
D、向右平行移动
|