题目内容
(坐标系与参数方程选做题)在平面直角坐标系中,直线l的参数方程为
(参数t∈R),圆的参数方程为
(参数θ∈[0,2π)),则圆心到直线l的距离为 .
|
|
考点:直线的参数方程
专题:坐标系和参数方程
分析:先把参数方程化为普通方程,然后利用点到直线的距离公式求得圆心到直线l的距离即可.
解答:
解:直线l的参数方程
化为普通方程为x+y-6=0,
圆的参数方程
化为普通方程为 x2+(y-1)2=4,
表示以(0,1)为圆心,半径等于2的圆.
则圆心到直线l的距离为d=
=
,
故答案为:
|
圆的参数方程
|
表示以(0,1)为圆心,半径等于2的圆.
则圆心到直线l的距离为d=
| |0+1-6| | ||
|
5
| ||
| 2 |
故答案为:
5
| ||
| 2 |
点评:本题考查把参数方程化为普通方程的方法,点到直线的距离公式的应用,属基础题.

练习册系列答案
相关题目
到空间不共面的四点距离相等的平面的个数为( )
| A、1个 | B、4个 | C、7个 | D、8个 |
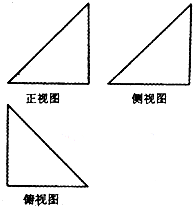 如图,某几何体的三视图均为腰长为1的等腰直角三角形,则此几何体最长的棱长为
如图,某几何体的三视图均为腰长为1的等腰直角三角形,则此几何体最长的棱长为