题目内容
已知弹道曲线的参数方程为
,g是重力加速度.
(1)求发射角α=
时,弹道曲线的普通方程和射程;
(2)设v0是定值,α是变量,求证:α=
时射程最大.
|
(1)求发射角α=
| π |
| 3 |
(2)设v0是定值,α是变量,求证:α=
| π |
| 4 |
考点:参数方程化成普通方程,函数的最值及其几何意义
专题:坐标系和参数方程
分析:(1)发射角α=
时,可得x=v0tcos
=
v0t,y=v0tsin
-
gt2=
v0t-
gt2,消去t可得y=
x-
.令y=0,可得x.
(2)由弹道曲线的参数方程
,g是重力加速度.消去t可得y=xtanα-
,令y=0,可得x=
sin2α,即可证明.
| π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 2gx2 | ||
|
(2)由弹道曲线的参数方程
|
| gx2 | ||
2
|
| ||
| g |
解答:
(1)解:发射角α=
时,x=v0tcos
=
v0t,y=v0tsin
-
gt2=
v0t-
gt2,
消去t可得y=
x-
.
令y=0,可得x=
.
(2)证明:由弹道曲线的参数方程
,g是重力加速度.消去t可得y=xtanα-
,
令y=0,可得x=
sin2α≤
,当且仅当α=
时射程最大.
| π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
消去t可得y=
| 3 |
| 2gx2 | ||
|
令y=0,可得x=
| ||||
| 2g |
(2)证明:由弹道曲线的参数方程
|
| gx2 | ||
2
|
令y=0,可得x=
| ||
| g |
| ||
| g |
| π |
| 4 |
点评:本题考查了弹道曲线的参数方程化为普通方程、三角函数的单调性,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
到空间不共面的四点距离相等的平面的个数为( )
| A、1个 | B、4个 | C、7个 | D、8个 |
已知
=(-1,2),
=(2,λ),且
与
的夹角为钝角,则实数λ的取值范围是( )
| a |
| b |
| a |
| b |
| A、(-∞,1) |
| B、(0,1) |
| C、(1,∞) |
| D、(-∞,-4)∪(-4,1) |
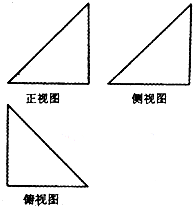 如图,某几何体的三视图均为腰长为1的等腰直角三角形,则此几何体最长的棱长为
如图,某几何体的三视图均为腰长为1的等腰直角三角形,则此几何体最长的棱长为