题目内容
已知α∈(0,π),且sinα+cosα=
,则sinα-cosα的值为( )
| ||
| 2 |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
考点:两角和与差的正弦函数
专题:三角函数的求值
分析:依题意,可得2sinαcosα=-
<0,又α∈(0,π),于是得sinα>0,cosα<0,sinα-cosα>0,对所求的关系式平方后再开方即可.
| 1 |
| 2 |
解答:
解:∵sinα+cosα=
,
∴(sinα+cosα)2=1+2sinαcosα=
,
∴2sinαcosα=-
<0,又α∈(0,π),
∴sinα>0,cosα<0,
∴sinα-cosα>0,
∵(sinα-cosα)2=1-2sinαcosα=
,
∴sinα-cosα=
.
故选:D.
| ||
| 2 |
∴(sinα+cosα)2=1+2sinαcosα=
| 1 |
| 2 |
∴2sinαcosα=-
| 1 |
| 2 |
∴sinα>0,cosα<0,
∴sinα-cosα>0,
∵(sinα-cosα)2=1-2sinαcosα=
| 3 |
| 2 |
∴sinα-cosα=
| ||
| 2 |
故选:D.
点评:本题考查同角三角函数间的关系,判断出sinα-cosα>0是关键,考查运算求解能力,属于中档题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
下面四个推导过程符合演绎推理三段论形式且推理正确的是( )
| A、大前提:无限不循环小数是无理数;小前提:π丌是无理数;结论:π是无限不循环小数 |
| B、大前提:无限不循环小数是无理数;小前提:π是无限不循环小数;结论:π是无理数 |
| C、大前提:π是无限不循环小数;小前提:无限不循环小数是无理数;结论:π是无理数 |
| D、大前提:π是无限不循环小数;小前提:π是无理数;结论:无限不循环小数是无理数 |
已知AB∥PQ,BC∥QR,∠ABC=60°,则∠PQR等于( )
| A、60° |
| B、60°或120° |
| C、120° |
| D、以上结论都不对 |
到空间不共面的四点距离相等的平面的个数为( )
| A、1个 | B、4个 | C、7个 | D、8个 |
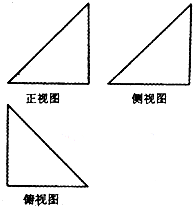 如图,某几何体的三视图均为腰长为1的等腰直角三角形,则此几何体最长的棱长为
如图,某几何体的三视图均为腰长为1的等腰直角三角形,则此几何体最长的棱长为