题目内容
19.在一次植树活动中,四名同学分别种植5棵树苗,每棵树苗成活的概率为$\frac{1}{2}$.如果一名同学种植的5棵树苗中至少3棵树苗成活,则认为该名同学植树活动成绩合格,否则认为该名同学植树活动成绩不合格.某名同学植树活动成绩不合格时,需要进行一次补种树苗,假设每人的补种树苗费用均为50元.(1)求四名同学中恰有两名同学需要补种树苗的概率;
(2)设X为需要补种树苗的人数,Y为补种树苗的总费用,求X的分布列和Y的期望.
分析 (1)一名同学需要进行补种树苗的概率为${∁}_{5}^{0}(\frac{1}{2})^{5}$+${∁}_{5}^{1}(\frac{1}{2})^{5}$+${∁}_{5}^{2}(\frac{1}{2})^{5}$.利用二项分布列的概率计算公式可得四名同学中恰有两名同学需要补种树苗的概率.
(2)由X~B$(4,\frac{1}{2})$,P(X=k)=${∁}_{4}^{k}(\frac{1}{2})^{k}(\frac{1}{2})^{4-k}$,可得X的分布列及其E(X).而Y=50X,可得E(Y)=50E(X).
解答 解:(1)一名同学需要进行补种树苗的概率为${∁}_{5}^{0}(\frac{1}{2})^{5}$+${∁}_{5}^{1}(\frac{1}{2})^{5}$+${∁}_{5}^{2}(\frac{1}{2})^{5}$=$\frac{1}{2}$.
则四名同学中恰有两名同学需要补种树苗的概率P=${∁}_{4}^{2}×(\frac{1}{2})^{2}×(\frac{1}{2})^{2}$=$\frac{3}{8}$.
(2)由X~B$(4,\frac{1}{2})$,P(X=k)=${∁}_{4}^{k}(\frac{1}{2})^{k}(\frac{1}{2})^{4-k}$,
则P(X=0)=$\frac{1}{16}$,P(X=1)=$\frac{1}{4}$,P(X=2)=$\frac{3}{8}$,P(X=3)=$\frac{1}{4}$.
P(X=4)=$\frac{1}{16}$.
X的分布列为:
| X | 0 | 1 | 2 | 3 | 4 |
| P | $\frac{1}{16}$ | $\frac{1}{4}$ | $\frac{3}{8}$ | $\frac{1}{4}$ | $\frac{1}{16}$ |
而Y=50X,∴E(Y)=50E(X)=50×2=100.
点评 本题考查了二项分布列的概率与数学期望计算公式及其性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
10.(理)已知是虚数单位,若$\frac{3+ai}{1-i}$是纯序数,则实数a的值为( )
| A. | 3 | B. | -3 | C. | 2 | D. | -2 |
14.直线2x+my=2m-4与直线mx+2y=m-2平行的充要条件是( )
| A. | m=0 | B. | m=±2 | C. | m=2 | D. | m=-2 |
4.已知α为锐角,且sinα=$\frac{4}{5}$,则cos(π+α)=( )
| A. | 一$\frac{3}{5}$ | B. | $\frac{3}{5}$ | C. | -$\frac{4}{5}$ | D. | $\frac{4}{5}$ |
1. 运行下列程序,当输入数值-2时,输出结果是( )
运行下列程序,当输入数值-2时,输出结果是( )
 运行下列程序,当输入数值-2时,输出结果是( )
运行下列程序,当输入数值-2时,输出结果是( )| A. | 7 | B. | 3 | C. | 0 | D. | -16 |
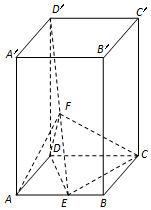 如图,底面为平行四边形的四棱柱ABCD-A'B'C'D'中,DD'⊥平面ABCD,∠DAB=$\frac{π}{3}$,AB=2AD,DD'=3AD,E、F分别是线段AB、D'E的中点.
如图,底面为平行四边形的四棱柱ABCD-A'B'C'D'中,DD'⊥平面ABCD,∠DAB=$\frac{π}{3}$,AB=2AD,DD'=3AD,E、F分别是线段AB、D'E的中点.