题目内容
7.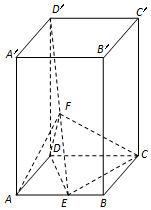 如图,底面为平行四边形的四棱柱ABCD-A'B'C'D'中,DD'⊥平面ABCD,∠DAB=$\frac{π}{3}$,AB=2AD,DD'=3AD,E、F分别是线段AB、D'E的中点.
如图,底面为平行四边形的四棱柱ABCD-A'B'C'D'中,DD'⊥平面ABCD,∠DAB=$\frac{π}{3}$,AB=2AD,DD'=3AD,E、F分别是线段AB、D'E的中点.(Ⅰ)求证:CE⊥DF;
(Ⅱ)求四棱锥F-AECD与四棱柱ABCD-A'B'C'D'的体积之比.
分析 (Ⅰ)由已知可得底面中DE⊥EC,再由DD'⊥平面ABCD得CE⊥D'D,然后利用线面垂直的判定可得CE⊥平面D'DE,从而得到CE⊥DF;
(Ⅱ)设出AD的长度,然后由已知求出四边形ABCD与梯形AECD的面积,再由F为D'E的中点即可求得四棱锥F-AECD与四棱柱ABCD-A'B'C'D'的体积之比.
解答 (Ⅰ)证明:由题意,AD=AE,$∠DAB=\frac{π}{3}$,
∴△DAE是等边三角形,在△BEC中,求得$∠BEC=\frac{π}{6}$,
则$∠DEC=\frac{π}{2}$,即CE⊥DE,
∵DD'⊥平面ABCD,∴CE⊥D'D,又DE∩DD′=D,∴CE⊥平面D'DE,
∵DF?平面D'DE,
∴CE⊥DF;
(Ⅱ)解:设AD=2,
∵△DAE是等边三角形,∴平行四边形ABCD的边AB上的高$h=\sqrt{3}$.
∴${S_{平行四边形ABCD}}=4\sqrt{3}$,${S_{梯形AECD}}=\frac{(2+4)}{2}×\sqrt{3}=3\sqrt{3}$,
∵F为D'E的中点,DD'⊥平面ABCD,
∴四棱锥F-AECD的底面ABCD上的高为$\frac{1}{2}DD'=3$.
∴$\frac{{{V_{F-AECD}}}}{{{V_{ABCD-A'B'C'D'}}}}=\frac{{\frac{1}{3}×3\sqrt{3}×3}}{{4\sqrt{3}×6}}=\frac{1}{8}$.
即四棱锥F-AECD与四棱柱ABCD-A'B'C'D'的体积之比为1:8.
点评 本题考查直线与平面垂直的判定和性质,考查空间想象能力和思维能力,训练了棱柱、棱锥及棱台体积的求法,是中档题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
18.设集合M={x∈R|x2<4},N={-1,1,2},则M∩N=( )
| A. | {-1,1,2} | B. | {-1,2} | C. | {1,2} | D. | {-1,1} |
2.若点P(x,y)是区域$\left\{\begin{array}{l}1≤x+y≤3\\ 1≤y-x≤3\end{array}\right.$内的任意一点,且为直线y=kx上的点,则实数k的取值范围是( )
| A. | $[-\frac{1}{2},\frac{1}{2}]$ | B. | [-2,2] | C. | (-∞,-2]∪[2,+∞) | D. | $(-∞,-\frac{1}{2}]∪[\frac{1}{2},+∞)$ |
12.复数z=|$\frac{\sqrt{3}+i}{i}$|+i3,i为虚数单位,则z的共轭复数为( )
| A. | 4-i | B. | 2-i | C. | 4+i | D. | 2+i |
16.程序框图如图所示,若运行结果输出s=120,则判断框内应填入( )


| A. | n≥5? | B. | n≤5? | C. | n≥4? | D. | n≤4? |