题目内容
9.已知数列{an}的前n项和为Sn,且满足Sn=2an-2,若数列{bn}满足bn=10-log2an,则使数列{bn}的前n项和取最大值时的n的值为9或10.分析 Sn=2an-2,n=1时,a1=2a1-2,解得a1.n≥2时,an=Sn-Sn-1,再利用等比数列的通项公式可得an.令bn≥0,解得n,即可得出.
解答 解:∵Sn=2an-2,∴n=1时,a1=2a1-2,解得a1=2.
n≥2时,an=Sn-Sn-1=2an-2-(2an-1-2),∴an=2an-1.
∴数列{an}是等比数列,公比为2.
∴an=2n.
∴bn=10-log2an=10-n.
由bn=10-n≥0,解得n≤10.
∴使数列{bn}的前n项和取最大值时的n的值为9或10.
故答案为:9或10.
点评 本题考查了数列递推关系、等比数列的通项公式、不等式的解法、数列的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
19.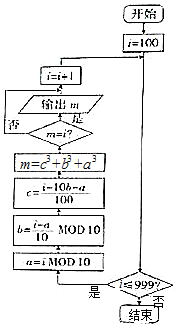 运行如图所示的程序框图,输出的数称为“水仙花数”.(算术符号MOD表示取余数,如11MOD2=1).下列数中的“水仙花数”是( )
运行如图所示的程序框图,输出的数称为“水仙花数”.(算术符号MOD表示取余数,如11MOD2=1).下列数中的“水仙花数”是( )
①“水仙花数”是三位数;
②152是“水仙花数”;
③407是“水仙花数”.
 运行如图所示的程序框图,输出的数称为“水仙花数”.(算术符号MOD表示取余数,如11MOD2=1).下列数中的“水仙花数”是( )
运行如图所示的程序框图,输出的数称为“水仙花数”.(算术符号MOD表示取余数,如11MOD2=1).下列数中的“水仙花数”是( )①“水仙花数”是三位数;
②152是“水仙花数”;
③407是“水仙花数”.
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
4.下列函数中为偶函数的是( )
| A. | y=x2sinx | B. | y=2-x | C. | y=$\frac{sinx}{x}$ | D. | y=|log0.5x| |
18.设集合M={x∈R|x2<4},N={-1,1,2},则M∩N=( )
| A. | {-1,1,2} | B. | {-1,2} | C. | {1,2} | D. | {-1,1} |
 已知三棱柱ABC-A1B1C1中,AB=AC=AA1=2,侧面ABB1A1⊥底面ABC,D是BC的中点,∠BAA1=120o,B1D⊥AB.
已知三棱柱ABC-A1B1C1中,AB=AC=AA1=2,侧面ABB1A1⊥底面ABC,D是BC的中点,∠BAA1=120o,B1D⊥AB.