题目内容
14.直线2x+my=2m-4与直线mx+2y=m-2平行的充要条件是( )| A. | m=0 | B. | m=±2 | C. | m=2 | D. | m=-2 |
分析 由m2-4=0,解得m=±2,经过验证即可得出.
解答 解:由m2-4=0,解得m=±2,
经过验证m=2时两条直线重合,舍去.
∴m=-2.
故选:D.
点评 本题考查了直线平行的充要条件、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
4.下列函数中为偶函数的是( )
| A. | y=x2sinx | B. | y=2-x | C. | y=$\frac{sinx}{x}$ | D. | y=|log0.5x| |
2.若点P(x,y)是区域$\left\{\begin{array}{l}1≤x+y≤3\\ 1≤y-x≤3\end{array}\right.$内的任意一点,且为直线y=kx上的点,则实数k的取值范围是( )
| A. | $[-\frac{1}{2},\frac{1}{2}]$ | B. | [-2,2] | C. | (-∞,-2]∪[2,+∞) | D. | $(-∞,-\frac{1}{2}]∪[\frac{1}{2},+∞)$ |
9.一种电子抽奖方式是:一次抽奖点击四次按钮,每次点击后,随机出现数字1,2,3,4.当出现的四个数字不重复,且相邻两数字不是连续数字(即两个数字差的绝对值为1)时,获头奖,则第一次抽奖获头奖的概率为( )
| A. | $\frac{1}{128}$ | B. | $\frac{3}{256}$ | C. | $\frac{1}{64}$ | D. | $\frac{1}{12}$ |
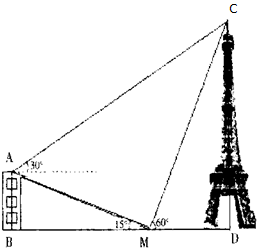 如图,一栋建筑物AB高(30-10$\sqrt{3}$)m,在该建筑 物的正东方向有一个通信塔CD.在它们之间的地面M点(B、M、D三点共线)测得对楼顶A、塔顶C的仰角分别是15°和60°,在楼顶A处 测得对塔顶C的仰角为30°,则通信塔CD的高为60m.
如图,一栋建筑物AB高(30-10$\sqrt{3}$)m,在该建筑 物的正东方向有一个通信塔CD.在它们之间的地面M点(B、M、D三点共线)测得对楼顶A、塔顶C的仰角分别是15°和60°,在楼顶A处 测得对塔顶C的仰角为30°,则通信塔CD的高为60m.