题目内容
11.已知△ABC中,AC=$\sqrt{2}$,BC=$\sqrt{6}$,△ABC的面积为$\frac{{\sqrt{3}}}{2}$,若线段BA的延长线上存在点D,使∠BDC=$\frac{π}{4}$,则CD=$\sqrt{3}$.分析 由已知利用三角形面积公式可求sin∠ACB=$\frac{1}{2}$,从而可求∠ACB=$\frac{π}{6}$,在△ABC中,由余弦定理可得AB,进而可求∠B,在△BCD中,由正弦定理可得CD的值.
解答 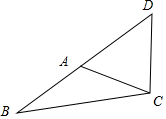 解:∵AC=$\sqrt{2}$,BC=$\sqrt{6}$,△ABC的面积为$\frac{{\sqrt{3}}}{2}$=$\frac{1}{2}$AC•BC•sin∠ACB=$\frac{1}{2}×\sqrt{2}×\sqrt{6}×$sin∠ACB,
解:∵AC=$\sqrt{2}$,BC=$\sqrt{6}$,△ABC的面积为$\frac{{\sqrt{3}}}{2}$=$\frac{1}{2}$AC•BC•sin∠ACB=$\frac{1}{2}×\sqrt{2}×\sqrt{6}×$sin∠ACB,
∴sin∠ACB=$\frac{1}{2}$,
∴∠ACB=$\frac{π}{6}$,或$\frac{5π}{6}$,
∵若∠ACB=$\frac{5π}{6}$,∠BDC=$\frac{π}{4}$<∠BAC,可得:∠BAC+∠ACB>$\frac{π}{4}$+$\frac{5π}{6}$>π,与三角形内角和定理矛盾,
∴∠ACB=$\frac{π}{6}$,
∴在△ABC中,由余弦定理可得:AB=$\sqrt{A{C}^{2}+B{C}^{2}-2AC•BC•cos∠ACB}$=$\sqrt{2+6-2×\sqrt{2}×\sqrt{6}×\frac{\sqrt{3}}{2}}$=$\sqrt{2}$,
∴∠B=$\frac{π}{6}$,
∴在△BCD中,由正弦定理可得:CD=$\frac{BC•sinB}{sin∠BDC}$=$\frac{\sqrt{6}×\frac{1}{2}}{\frac{\sqrt{2}}{2}}$=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题主要考查了三角形面积公式,余弦定理,正弦定理在解三角形中的应用,考查了转化思想和数形结合思想,求∠ACB的值是解题的关键,属于中档题.

 优等生题库系列答案
优等生题库系列答案| A. | $[-\frac{1}{2},\frac{1}{2}]$ | B. | [-2,2] | C. | (-∞,-2]∪[2,+∞) | D. | $(-∞,-\frac{1}{2}]∪[\frac{1}{2},+∞)$ |

| A. | n≥5? | B. | n≤5? | C. | n≥4? | D. | n≤4? |
| 日期 | 比赛队 | 主场 | 客场 | 比赛时间 | 比赛地点 |
| 17年3月10日 | 新疆-辽宁 | 新疆 | 辽宁 | 20:00 | 乌鲁木齐 |
| 17年3月12日 | 新疆-辽宁 | 新疆 | 辽宁 | 20:00 | 乌鲁木齐 |
| 17年3月15日 | 辽宁-新疆 | 辽宁 | 新疆 | 20:00 | 本溪 |
| 17年3月17日 | 辽宁-新疆 | 辽宁 | 新疆 | 20:00 | 本溪 |
| 17年3月19日 | 辽宁-新疆 | 辽宁 | 新疆 | 20:00 | 本溪 |
| 17年3月22日 | 新疆-辽宁 | 新疆 | 辽宁 | 20:00 | 乌鲁木齐 |
| 17年3月24日 | 新疆-辽宁 | 新疆 | 辽宁 | 20:00 | 乌鲁木齐 |
(2)根据以往资料统计,每场比赛组织者可获得门票收入50万元(与主客场无关),若不考虑主客场因素,每个队每场比赛获胜的概率均为$\frac{1}{2}$,设本次半决赛中(只考虑这两支队)组织者所获得的门票收入为X,求X的分布列及数学期望.
