题目内容
10．（理）已知是虚数单位，若$\frac{3+ai}{1-i}$是纯序数，则实数a的值为（ ）| A． | 3 | B． | -3 | C． | 2 | D． | -2 |
分析 直接由复数代数形式的乘除运算化简再结合已知条件列出方程组，求解即可得答案．
解答 解：∵$\frac{3+ai}{1-i}$=$\frac{（3+ai）（1+i）}{（1-i）（1+i）}=\frac{3-a+（3+a）i}{2}$=$\frac{3-a}{2}+\frac{3+a}{2}i$是纯虚数，
∴$\left\{\begin{array}{l}{\frac{3-a}{2}=0}\\{\frac{3+a}{2}≠0}\end{array}\right.$，
解得：a=3．
故选：A．
点评 本题考查了复数代数形式的乘除运算，考查了复数的基本概念，是基础题．
练习册系列答案
相关题目
已知三棱柱ABC-A1B1C1中，AB=AC=AA1=2，侧面ABB1A1⊥底面ABC，D是BC的中点，∠BAA1=120o，B1D⊥AB．
18．设集合M={x∈R|x2＜4}，N={-1，1，2}，则M∩N=（ ）
| A． | {-1，1，2} | B． | {-1，2} | C． | {1，2} | D． | {-1，1} |
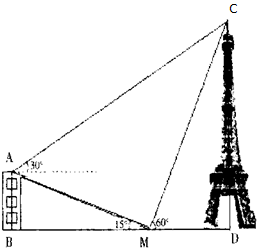如图，一栋建筑物AB高（30-10$\sqrt{3}$）m，在该建筑 物的正东方向有一个通信塔CD．在它们之间的地面M点（B、M、D三点共线）测得对楼顶A、塔顶C的仰角分别是15°和60°，在楼顶A处 测得对塔顶C的仰角为30°，则通信塔CD的高为60m．
2．若点P（x，y）是区域$\left\{\begin{array}{l}1≤x+y≤3\\ 1≤y-x≤3\end{array}\right.$内的任意一点，且为直线y=kx上的点，则实数k的取值范围是（ ）
| A． | $[-\frac{1}{2}，\frac{1}{2}]$ | B． | [-2，2] | C． | （-∞，-2]∪[2，+∞） | D． | $（-∞，-\frac{1}{2}]∪[\frac{1}{2}，+∞）$ |