题目内容
2.已知三个命题p,q,m中只有一个是真命题,课堂上老师给出了三个判断:A:p是真命题;B:p∨q是假命题;C:m是真命题.
老师告诉学生三个判断中只有一个是错误的,那么三个命题p,q,m中的真命题是m.
分析 根据已知中老师告诉学生三个判断中只有一个是错误的,逐一分析论证,可得答案.
解答 解:由已知中三个命题p,q,m中只有一个是真命题,
①若A是错误的,则:
p是假命题;q是假命题;m是真命题.满足条件;
②若B是错误的,则:
p是真命题;q的真假不能确定;m是真命题.不满足条件;
③若C是错误的,则:
p是真命题;p∨q不可能是假命题;不满足条件;
故真命题是m,
故答案为:m
点评 本题以命题的真假判断与应用为载体,考查了复合命题的真假判断,难度中档.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
10.已知等比数列{an}的公比q=2,a4=8,Sn为{an}的前n项和,设a=a20.3,b=0.3${\;}^{{a}_{3}}$,c=logan(Sn+$\frac{1}{{S}_{n}}$),则a,b,c大小关系是( )
| A. | a<b<c | B. | b<a<c | C. | c<b<a | D. | b<c<a |
14.北京时间3月10日,CBA半决赛开打,采用7局4胜制(若某对取胜四场,则终止本次比赛,并获得进入决赛资格),采用2-3-2的赛程,辽宁男篮将与新疆男篮争夺一个决赛名额,由于新疆队常规赛占优,决赛时拥有主场优势(新疆先两个主场,然后三个客场,再两个主场),以下是总决赛赛程:
(1)若考虑主场优势,每个队主场获胜的概率均为$\frac{2}{3}$,客场取胜的概率均为$\frac{1}{3}$,求辽宁队以比分4:1获胜的概率;
(2)根据以往资料统计,每场比赛组织者可获得门票收入50万元(与主客场无关),若不考虑主客场因素,每个队每场比赛获胜的概率均为$\frac{1}{2}$,设本次半决赛中(只考虑这两支队)组织者所获得的门票收入为X,求X的分布列及数学期望.
| 日期 | 比赛队 | 主场 | 客场 | 比赛时间 | 比赛地点 |
| 17年3月10日 | 新疆-辽宁 | 新疆 | 辽宁 | 20:00 | 乌鲁木齐 |
| 17年3月12日 | 新疆-辽宁 | 新疆 | 辽宁 | 20:00 | 乌鲁木齐 |
| 17年3月15日 | 辽宁-新疆 | 辽宁 | 新疆 | 20:00 | 本溪 |
| 17年3月17日 | 辽宁-新疆 | 辽宁 | 新疆 | 20:00 | 本溪 |
| 17年3月19日 | 辽宁-新疆 | 辽宁 | 新疆 | 20:00 | 本溪 |
| 17年3月22日 | 新疆-辽宁 | 新疆 | 辽宁 | 20:00 | 乌鲁木齐 |
| 17年3月24日 | 新疆-辽宁 | 新疆 | 辽宁 | 20:00 | 乌鲁木齐 |
(2)根据以往资料统计,每场比赛组织者可获得门票收入50万元(与主客场无关),若不考虑主客场因素,每个队每场比赛获胜的概率均为$\frac{1}{2}$,设本次半决赛中(只考虑这两支队)组织者所获得的门票收入为X,求X的分布列及数学期望.
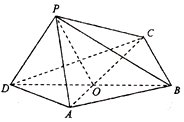 如图,四边形ABCD中,△BCD为正三角形,AD=AB=2,BD=2$\sqrt{3}$,AC与BD交于O点.将△ACD沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为θ,且P点在平面ABCD内的射影落在△ACD内.
如图,四边形ABCD中,△BCD为正三角形,AD=AB=2,BD=2$\sqrt{3}$,AC与BD交于O点.将△ACD沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为θ,且P点在平面ABCD内的射影落在△ACD内.