题目内容
20.已知函数f(x)=$\left\{\begin{array}{l}{1,x∈Q}\\{0,x∈{∁}_{R}Q}\end{array}\right.$,则f(f(2π))=1.分析 先求出f(2π)=0,从而f(f(2π))=f(0),由此能求出结果.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}{1,x∈Q}\\{0,x∈{∁}_{R}Q}\end{array}\right.$,
∴f(2π)=0,
f(f(2π))=f(0)=1.
故答案为:1.
点评 本题考查函数值的求法,考查实数的取值范围的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
15.若x=1是函数f(x)=$\frac{a}{x}$+b(a≠0)的一个零点,则函数h(x)=ax2+bx的零点是( )
| A. | 0或-1 | B. | 0或-2 | C. | 0或1 | D. | 0或2 |
19.已知F1,F2是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点,过F1的直线l与双曲线的左右两支分别交于点A、B,若△ABF2是以∠ABF2为顶点的等腰直角三角形,则双曲线的离心率的平方为( )
| A. | 5+2$\sqrt{2}$ | B. | 4+2$\sqrt{2}$ | C. | $\sqrt{7}$ | D. | 3+2$\sqrt{2}$ |
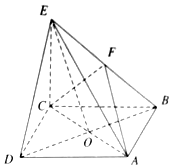 在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.
在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.