题目内容
10.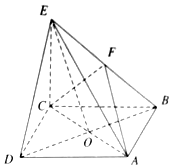 在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.
在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.(Ⅰ)求证:DE∥平面ACF;
(Ⅱ)求证:BD⊥AE;
(Ⅲ)若AB=$\sqrt{2}$CE=2,求三棱锥F-ABC的体积.
分析 (Ⅰ)利用线面平行的判定定理证明DE∥平面ACF;
(Ⅱ)利用线面垂直的判定定理先证明BD⊥平面ACE,然后利用线面垂直的性质证明BD⊥AE;
(Ⅲ)取BC中G,连结FG,推导出FG⊥底面ABCD,由此能求出三棱锥F-ABC的体积.
解答 证明:(Ⅰ)连接OF.由ABCD是正方形可知,点O为BD中点.
又F为BE的中点,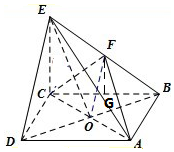 ∴OF∥DE.
∴OF∥DE.
又OF?面ACF,DE?面ACF,
∴DE∥平面ACF….(4分)
(II)由EC⊥底面ABCD,BD?底面ABCD,
∴EC⊥BD,
由ABCD是正方形可知,AC⊥BD,
又AC∩EC=C,AC、E?平面ACE,
∴BD⊥平面ACE,
又AE?平面ACE,
∴BD⊥AE…(9分)
解:(III)取BC中G,连结FG,
在四棱锥E-ABCD中,EC⊥底面ABCD,
∵FG是△BCE的中位线,∴FG⊥底面ABCD,
∵AB=$\sqrt{2}CE=2$,∴FG=$\frac{1}{2}EC=\frac{\sqrt{2}}{2}$,
∴三棱锥F-ABC的体积V=$\frac{1}{3}×{S}_{△ABC}×FG$=$\frac{1}{3}$×$\frac{1}{2}$×4×$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}}{3}$.
点评 本题主要考查了空间直线和平面垂直的判定定理和性质定理的应用,要求熟练掌握相应的定理,是中档题.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
20.已知实数x,y满足$\left\{\begin{array}{l}{x-2y+1>0}\\{x<2}\\{x+y-1>0}\end{array}\right.$,若z=2x-2y-1,则z的取值范围为( )
| A. | (-$\frac{5}{3}$,5) | B. | (-$\frac{5}{3}$,0) | C. | [0,5] | D. | [-$\frac{5}{3}$,5] |
18.设抛物线C:y2=2px(p>0)的焦点F,其准线与x轴相交于点Q,过点F倾斜角为锐角θ的直线交抛物线于A,B两点,若∠QBF=90°,则cosθ=$\frac{\sqrt{5}-1}{2}$.
15.已知正三棱锥P-ABC的底面ABC的边长为a,高为h,在正三棱锥内任取一点M,使得VP-ABC>2VM-ABC的概率是( )
| A. | $\frac{7}{8}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
2.不等式x2-1≥0的解集为( )
| A. | {x|-1≤x≤1} | B. | {x|-1<x<1} | C. | {x|x≥1或x≤-1} | D. | {x|x>1或x<-1} |