Question

设x，y，a都是实数，且x+y=2a-1，x²+y²=a²+2a-3，求乘积xy的最小值及相应的a的值．

Answer 1

考点：基本不等式

专题：不等式的解法及应用

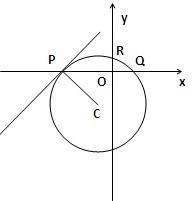
分析：由于x²+y²=a²+2a-3，可知：a²+2a-3≥0，解得a≥1或a≤-3．若直线x+y=2a-1与上述圆有公共点，则

|2a-1|

2

≤

a2+2a-3

，可得a取值范围，利用xy=

(x+y)2-(x2+y2)

2

代入整理为xy=

3

2

(a-1)2+

1

2

．利用二次函数的单调性即可得出．

解答： 解：∵x²+y²=a²+2a-3，
∴a²+2a-3≥0，解得a≥1或a≤-3．（*）
若直线x+y=2a-1与上述圆有公共点，则

|2a-1|

2

≤

a2+2a-3

，
解得

4- 2

2

≤a≤

4+ 2

2

，可知满足（*）．
∴a的取值范围是[

4- 2

2

，

4+ 2

2

]．
又xy=

(x+y)2-(x2+y2)

2

=

(2a-1)2-(a2+2a-3)

2

=

3

2

a2+3a+2．
∴xy=

3

2

(a-1)2+

1

2

．
当a≥1时，函数f（a）=

3

2

(a-1)2+

1

2

单调递增．
而

4- 2

2

≤a≤

4+ 2

2

，∴当a=

4- 2

2

时，xy取得最小值

3

2

(

4- 2

2

-1)2+

1

2

，即为

11-6 2

4

．
综上可知：当且仅当a=

4- 2

2

时，xy取得最小值

11-6 2

4

．

点评：本题综合考查了一元二次不等式的解法、分类讨论、二次函数的单调性，属于中档题．