Question

如图，圆C通过不同的三点P（m，0）、Q（2，0）、R（0，1），且圆C在点P处的切线的斜率为1，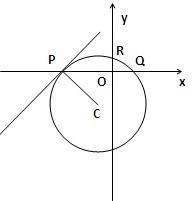
（Ⅰ）试求圆C的方程．
（Ⅱ）若点A、B是圆C上不同两点，且满足

CP

•

CA

=

CP

•

CB

．
（1）试求直线AB的斜率；
（2）若原点O在以AB为直径的圆的内部，试求直线AB在y轴上的截距的范围．

Answer 1

考点：直线和圆的方程的应用,平面向量数量积的运算,直线的斜率,圆的一般方程

专题：综合题,直线与圆

分析：（Ⅰ）设圆C的方程为x²+y²+Dx+Ey+F=0，根据圆C通过不同的三点P（m，0）、Q（2，0）、R（0，1），PC的斜率为-1，求出D，E，F，即可求圆C的方程．
（Ⅱ）（1）设A（x₁，y₁），B（x₂，y₂），由

CP

•

CA

=

CP

•

CB

，可得x₁-y₁=x₂-y₂，即可求直线AB的斜率；
（2）设直线AB的方程为y=x+t，代入圆C的方程为x²+y²+x+5y-6=0得2x²+（2t+6）x+t²+5t-6=0，由题意△＞0，解得-7＜t＜4，根据原点O在以AB为直径的圆的内部，可得

OA

•

OB

＜0，即x₁x₂+y₁y₂＜0，从而可求直线AB在y轴上的截距的范围．

解答： 解：（Ⅰ）设圆C的方程为x²+y²+Dx+Ey+F=0
则C点的坐标为(-

D

2

，-

E

2

)，且PC的斜率为-1，（3分）
因为圆C通过不同的三点P（m，0）、Q（2，0）、R（0，1）
所以有

1+E+F=0 4+2D+F=0 - D 2 = 2+m 2 - E 2 -0 - D 2 -m =-1

解之得

D=1 E=5 F=-6 m=-3

（8分）
所以圆C的方程为x²+y²+x+5y-6=0
（Ⅱ）（1）因为C(-

1

2

，-

5

2

)，P（-3，0），
所以

CP

=(-

5

2

，

5

2

)
设A（x₁，y₁），B（x₂，y₂），
则

CA

=(x1+

1

2

，y1+

5

2

)，

CB

=(x2+

1

2

，y2+

5

2

)（10分）
由

CP

•

CA

=

CP

•

CB

，
得-

5

2

(x1+

1

2

)+

5

2

(y1+

5

2

)=-

5

2

(x2+

1

2

)+

5

2

(y2+

5

2

)，
即x₁-y₁=x₂-y₂，∴kAB=

y2-y1

x2-x1

=1．
（2）设直线AB在y轴上的截距为t，则直线AB的方程为y=x+t，
代入圆C的方程为x²+y²+x+5y-6=0得2x²+（2t+6）x+t²+5t-6=0（*）
由题意△=（2t+6）²-8（t²+5t-6）=-4t²-16t+84＞0，解得-7＜t＜4，
又原点O在以AB为直径的圆的内部，
所以

OA

•

OB

＜0，即x₁x₂+y₁y₂＜0，（14分）
所以x₁x₂+（x₁+t）（x₂+t）＜0，由（*）知，x1x2=

1

2

(t2+5t-6)，x₁+x₂=-t-3，
代入整理得，t²+2t-6＜0，解得-

7

-1＜t＜

7

-1，
综上，-

7

-1＜t＜

7

-1．（16分）

点评：本题考查圆的一般方程，考查直线与圆的位置关系，考查向量知识的运用，考查学生分析解决问题的能力，属于中档题．