题目内容
20．过圆x2+y2=1上任意一点P作x轴的垂线PN，垂足为N，则线段PN的中点M的轨迹方程为x2+4y2=1．分析 利用中点坐标公式，确定P，M坐标之间的关系，将P的坐标代入圆的方程，即可求得M的轨迹方程．
解答 解：设M（x，y），N（x，0）则P（x，2y）
∵P在圆x2+y2=1上，
∴x2+4y2=1，
∴故答案为：x2+4y2=1．
点评 本题考查了轨迹方程的求法，中点坐标公式，考查了代入法，属于基础题．
练习册系列答案
相关题目
10．已知A、B、C、D四点共线，$α∈（\frac{π}{2}，π）$，且向量$\overrightarrow{AB}=（tanα，1）$，$\overrightarrow{CD}=（3tan2α，-2）$，则$tan（2α-\frac{π}{4}）$等于（ ）
| A． | $-\frac{1}{7}$ | B． | $\frac{1}{7}$ | C． | -7 | D． | 7 |
11．已知命题p：“?x∈（0，+∞），lnx+4x≥3”；命题q：“?x0∈（0，+∞），8x0+$\frac{1}{2{x}_{0}}$≤4”．则下列命题为真命题的是（ ）
| A． | （￢p）∧q | B． | p∧q | C． | p∨（￢q） | D． | （￢p）∧（￢q） |
8．圆O1：x2+y2-2x=0和圆O2：x2+y2-4x=0的公切线条数（ ）
| A． | 1条 | B． | 2条 | C． | 3条 | D． | 4条 |
5．若函数f（x）=ax2+bx+c，a＞0，对任意实数x都有f（2+x）=f（2-x），那么（ ）
| A． | f（2）＜f（1）＜f（4） | B． | f（1）＜f（2）＜f（4） | C． | f（2）＜f（4）＜f（1） | D． | f（4）＜f（2）＜f（1） |
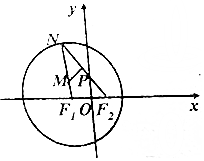已知F1为圆（x+1）2+y2=16的圆心，N为圆F1上一动点，且F2（1，0），点M，P分别是线段F1N，F2N上的点，满足$\overrightarrow{MP}$•$\overrightarrow{{F}_{2}N}$=0，$\overrightarrow{{F}_{2}N}$=2$\overrightarrow{{F}_{2}P}$．
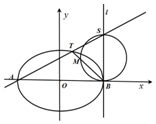已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的长轴长为2$\sqrt{2}$，离心率为$\frac{\sqrt{2}}{2}$．