��Ŀ����
10��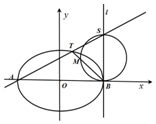 ��֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0���ij��᳤Ϊ2$\sqrt{2}$��������Ϊ$\frac{\sqrt{2}}{2}$��
��֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0���ij��᳤Ϊ2$\sqrt{2}$��������Ϊ$\frac{\sqrt{2}}{2}$����������ԲC�ı����̣�
������֪A��BΪ��Բ�������������㣬TΪ��Բ���ڵ�һ�����ڵ�һ�㣬lΪ����B�Ҵ�ֱx���ֱ�ߣ���SΪֱ��AT��ֱ��l�Ľ��㣬��M��SBΪֱ����Բ��ֱ��TB����һ�����㣬��֤��O��M��S���㹲�ߣ�
���� ������a����Բ�������ʹ�ʽ���cֵ����b2=a2-c2=1�����������Բ�ķ��̣�
������ֱ��AT�ķ��̣�������Բ���̣���Τ�ﶨ�����T�����꣬��BT��SM����$\overrightarrow{SO}$=��-$\sqrt{2}$��-2$\sqrt{2}$k������$\overrightarrow{SO}$•$\overrightarrow{BT}$=$\frac{8{k}^{2}-8{k}^{2}}{1+2{k}^{2}}$=0��BT��SO������O��M��S���㹲�ߣ�
��� �⣺����������֪��a=$\sqrt{2}$��e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$����c=1��
��b2=a2-c2=1��
����ԲC�ķ���Ϊ��$\frac{{x}^{2}}{2}+{y}^{2}=1$�� ����4�֣�
������ֱ��AT����Ϊ��y=k��x+$\sqrt{2}$������k��0�������T����Ϊ��x1��y1����
$\left\{\begin{array}{l}{y=k��x+\sqrt{2}��}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$����1+2k2��x2+4$\sqrt{2}$k2x+4k2-1=0������5�֣�
��Τ�ﶨ��x1x2=$\frac{4{k}^{2}-2}{1+2{k}^{2}}$����A������Ϊ��-$\sqrt{2}$��0����
��x1=$\frac{\sqrt{2}-2\sqrt{2}{k}^{2}}{1+2{k}^{2}}$��y1=$\frac{2\sqrt{2}k}{1+2{k}^{2}}$������7�֣�
��B������Ϊ��$\sqrt{2}$��0������$\overrightarrow{BT}$=��-$\frac{4\sqrt{2}{k}^{2}}{1+2{k}^{2}}$��$\frac{2\sqrt{2}k}{1+2{k}^{2}}$��������8�֣�
��Բ�����ʵã�BT��SM��
���ԣ�Ҫ֤��O��M��S���㹲��ֻҪ֤��BT��SO���ɣ�����9�֣�
��S�������Ϊ$\sqrt{2}$����S������Ϊ��$\sqrt{2}$��2$\sqrt{2}$k����$\overrightarrow{SO}$=��-$\sqrt{2}$��-2$\sqrt{2}$k����
$\overrightarrow{SO}$•$\overrightarrow{BT}$=$\frac{8{k}^{2}-8{k}^{2}}{1+2{k}^{2}}$=0������11�֣�
��BT��SO����BT��SM��
��O��M��S���㹲�ߣ�����12�֣�
���� ���⿼����Բ�ı����̼��������ʣ�����ֱ������Բ��λ�ù�ϵ������Τ�ﶨ�����������������������㣬������������������е��⣮

| A�� | $[{\frac{��}{12}��\frac{��}{4}}]$ | B�� | $[{\frac{��}{12}��\frac{5��}{12}}]$ | C�� | $[{\frac{��}{6}��\frac{��}{3}}]$ | D�� | $[{0��\frac{��}{2}}]$ |
| A�� | 5 | B�� | $\frac{5}{2}$ | C�� | $\frac{5}{4}$ | D�� | $\frac{5}{8}$ |
| A�� | y=��$\frac{9}{10}$x | B�� | y=��$\frac{10}{9}$x | C�� | y=��$\frac{{3\sqrt{10}}}{10}$x | D�� | y=��$\frac{{\sqrt{10}}}{3}$x |
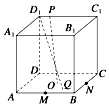 ��������ABCD-A1B1C1D1�У�PΪ������A1B1C1D1�ı��ϵĶ��㣬OΪ����������ABCD�����ģ�M��N�ֱ�ΪAB��BC���е㣬��QΪƽ��ABCD��һ�㣬�߶�D1Q��OP����ƽ�֣�������$\overrightarrow{MQ}$=��$\overrightarrow{MN}$��ʵ������2����
��������ABCD-A1B1C1D1�У�PΪ������A1B1C1D1�ı��ϵĶ��㣬OΪ����������ABCD�����ģ�M��N�ֱ�ΪAB��BC���е㣬��QΪƽ��ABCD��һ�㣬�߶�D1Q��OP����ƽ�֣�������$\overrightarrow{MQ}$=��$\overrightarrow{MN}$��ʵ������2����