题目内容
11.已知命题p:“?x∈(0,+∞),lnx+4x≥3”;命题q:“?x0∈(0,+∞),8x0+$\frac{1}{2{x}_{0}}$≤4”.则下列命题为真命题的是( )| A. | (¬p)∧q | B. | p∧q | C. | p∨(¬q) | D. | (¬p)∧(¬q) |
分析 分别判断出p,q的真假,从而判断出复合命题的真假即可.
解答 解:取x=$\frac{1}{2}$,可知lnx+4x<3,故命题p为假命题;
当x0>0时,8x0+$\frac{1}{{2x}_{0}}$≥2$\sqrt{{8x}_{0}•\frac{1}{{2x}_{0}}}$=4,
当且仅当x0=$\frac{1}{4}$时等号成立,故命题q为真命题;
所以(¬p)∧q为真命题,p∧q、p∨(¬q)、(¬p)∧(¬q)为假命题,
故选:A.
点评 本题考查了复合命题的判断,考查不等式的性质,是一道中档题.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
19.关于复数Z=$\frac{2}{-1+i}$的四个命题:
p1:|Z|=2
p2:Z2=2i
p3:Z的共轭复数为1+i
p4:Z的虚部为-1.
其中的真命题为( )
p1:|Z|=2
p2:Z2=2i
p3:Z的共轭复数为1+i
p4:Z的虚部为-1.
其中的真命题为( )
| A. | p2,p3 | B. | p1,p2 | C. | p2,p4 | D. | p3,p4 |
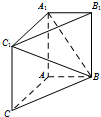 如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.
如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.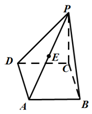 如图在边长为2的菱形ABCD中,∠ABC=60°,PC⊥平面ABCD,PC=2,E为PA的中点.(1)求证:平面EBD⊥平面ABCD;
如图在边长为2的菱形ABCD中,∠ABC=60°,PC⊥平面ABCD,PC=2,E为PA的中点.(1)求证:平面EBD⊥平面ABCD; 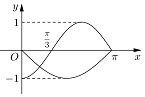 已知函数y=f(x)是偶函数,y=g(x)的奇函数,它们的定义域为[-π,π],且它们在x∈[0,π]上的图象如图所示,则不等式$\frac{f(x)}{g(x)}>0$的解集为$(-π,-\frac{π}{3})∪(0,\frac{π}{3})$.
已知函数y=f(x)是偶函数,y=g(x)的奇函数,它们的定义域为[-π,π],且它们在x∈[0,π]上的图象如图所示,则不等式$\frac{f(x)}{g(x)}>0$的解集为$(-π,-\frac{π}{3})∪(0,\frac{π}{3})$.