题目内容
10.已知A、B、C、D四点共线,$α∈(\frac{π}{2},π)$,且向量$\overrightarrow{AB}=(tanα,1)$,$\overrightarrow{CD}=(3tan2α,-2)$,则$tan(2α-\frac{π}{4})$等于( )| A. | $-\frac{1}{7}$ | B. | $\frac{1}{7}$ | C. | -7 | D. | 7 |
分析 利用向量共线定理可得tanα,再利用倍角公式与和差公式即可得出.
解答 解:∵A、B、C、D四点共线,$α∈(\frac{π}{2},π)$,且向量$\overrightarrow{AB}=(tanα,1)$,$\overrightarrow{CD}=(3tan2α,-2)$,
∴3tan2α+2tanα=0,化为:$\frac{6tanα}{1-ta{n}^{2}α}+2tanα$=0,tanα>0,
解得tanα=2,tan2α=-$\frac{4}{3}$.
则$tan(2α-\frac{π}{4})$=$\frac{tan2α-1}{1+tan2α}$=$\frac{-\frac{4}{3}-1}{1-\frac{4}{3}}$=7.
故选:D.
点评 本题考查了向量共线定理、倍角公式与和差公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
16.某空间几何体的三视图如图所示,则此几何体的体积为( )


| A. | $\frac{5π}{3}$ | B. | $\frac{10π}{3}$ | C. | $\frac{11π}{3}$ | D. | $\frac{22π}{3}$ |
19.关于复数Z=$\frac{2}{-1+i}$的四个命题:
p1:|Z|=2
p2:Z2=2i
p3:Z的共轭复数为1+i
p4:Z的虚部为-1.
其中的真命题为( )
p1:|Z|=2
p2:Z2=2i
p3:Z的共轭复数为1+i
p4:Z的虚部为-1.
其中的真命题为( )
| A. | p2,p3 | B. | p1,p2 | C. | p2,p4 | D. | p3,p4 |
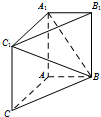 如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.
如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.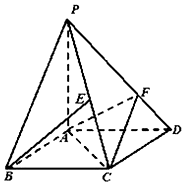 如图,四棱锥P-ABCD的底面ABCD是平行四边形,AD=2,AB=1,∠ABC=60°,PA⊥面ABCD,设E为PC中点,点F在线段PD上,且PF=2FD.
如图,四棱锥P-ABCD的底面ABCD是平行四边形,AD=2,AB=1,∠ABC=60°,PA⊥面ABCD,设E为PC中点,点F在线段PD上,且PF=2FD.