题目内容
8.圆O1:x2+y2-2x=0和圆O2:x2+y2-4x=0的公切线条数( )| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
分析 判断两个圆的位置关系,然后判断公切线条数.
解答 解:圆O1:x2+y2-2x=0的圆心(1,0)半径为1;圆O2:x2+y2-4x=0的圆心(2,0),半径为2,
O1O2=1=2-1,∴两个圆内切,
所以圆O1:x2+y2-2x=0和圆O2:x2+y2-4x=0的公切线条数:1.
故选:A.
点评 本题考查两个圆的位置关系,两个圆相离公切线4条,相交2条,外切3条,内切1条.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
19.关于复数Z=$\frac{2}{-1+i}$的四个命题:
p1:|Z|=2
p2:Z2=2i
p3:Z的共轭复数为1+i
p4:Z的虚部为-1.
其中的真命题为( )
p1:|Z|=2
p2:Z2=2i
p3:Z的共轭复数为1+i
p4:Z的虚部为-1.
其中的真命题为( )
| A. | p2,p3 | B. | p1,p2 | C. | p2,p4 | D. | p3,p4 |
17.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的渐近线方程为3x±4y=0,右焦点为(5,0),则双曲线C的方程为( )
| A. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{4}$=1 | B. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{3}$=1 | C. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1 | D. | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1 |
18.若圆x2+y2-6x-4y-5=0上至少有三个不同的点到直线?:ax+by-a=0的距离为2$\sqrt{2}$,则直线?倾斜角的取值范围是:( )
| A. | $[{\frac{π}{12},\frac{π}{4}}]$ | B. | $[{\frac{π}{12},\frac{5π}{12}}]$ | C. | $[{\frac{π}{6},\frac{π}{3}}]$ | D. | $[{0,\frac{π}{2}}]$ |
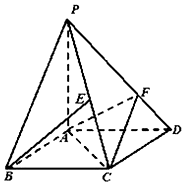 如图,四棱锥P-ABCD的底面ABCD是平行四边形,AD=2,AB=1,∠ABC=60°,PA⊥面ABCD,设E为PC中点,点F在线段PD上,且PF=2FD.
如图,四棱锥P-ABCD的底面ABCD是平行四边形,AD=2,AB=1,∠ABC=60°,PA⊥面ABCD,设E为PC中点,点F在线段PD上,且PF=2FD.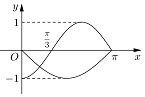 已知函数y=f(x)是偶函数,y=g(x)的奇函数,它们的定义域为[-π,π],且它们在x∈[0,π]上的图象如图所示,则不等式$\frac{f(x)}{g(x)}>0$的解集为$(-π,-\frac{π}{3})∪(0,\frac{π}{3})$.
已知函数y=f(x)是偶函数,y=g(x)的奇函数,它们的定义域为[-π,π],且它们在x∈[0,π]上的图象如图所示,则不等式$\frac{f(x)}{g(x)}>0$的解集为$(-π,-\frac{π}{3})∪(0,\frac{π}{3})$.