��Ŀ����
12��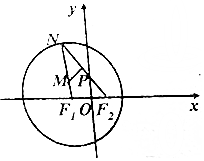 ��֪F1ΪԲ��x+1��2+y2=16��Բ�ģ�NΪԲF1��һ���㣬��F2��1��0������M��P�ֱ����߶�F1N��F2N�ϵĵ㣬����$\overrightarrow{MP}$•$\overrightarrow{{F}_{2}N}$=0��$\overrightarrow{{F}_{2}N}$=2$\overrightarrow{{F}_{2}P}$��
��֪F1ΪԲ��x+1��2+y2=16��Բ�ģ�NΪԲF1��һ���㣬��F2��1��0������M��P�ֱ����߶�F1N��F2N�ϵĵ㣬����$\overrightarrow{MP}$•$\overrightarrow{{F}_{2}N}$=0��$\overrightarrow{{F}_{2}N}$=2$\overrightarrow{{F}_{2}P}$��������M�Ĺ켣E�ķ��̣�
������F2��ֱ��l����x��غϣ���켣E����A��C���㣬�߶�AC���е�ΪG������OG���ӳ����켣E��B�㣨OΪ����ԭ�㣩�����ı���OABC�����S����Сֵ��
���� ����ȷ������M�Ĺ켣����F1��-1��0����F2��1��0��Ϊ�������Բ��������M�Ĺ켣E�ķ��̣�
������ֱ��AC�ķ���Ϊx=my+1������Բ�����������ɵã�4+3m2��y2+6my-9=0����ʾ���ı���OABC���������������ı���OABC�����S����Сֵ��
��� �⣺���������⣬MP��ֱƽ��F2N��
��|MF1|+|MF2|=4
���Զ���M�Ĺ켣����F1��-1��0����F2��1��0��Ϊ�������Բ����..��3�֣�
�ҳ��᳤Ϊ2a=4������2c=2������a=2��c=1��b2=3��
����E�ķ���Ϊ$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1��
������A��x1��y1����C��x2��y2����G��x0��y0����
��ֱ��AC�ķ���Ϊx=my+1������Բ�����������ɵã�4+3m2��y2+6my-9=0��
��y1+y2=-$\frac{6m}{4+3{m}^{2}}$��y1y2=-$\frac{9}{4+3{m}^{2}}$��
���ҳ���ʽ�ɵ�|AC|=$\sqrt{1+{m}^{2}}$|y1-y2|=$\frac{12��1+{m}^{2}��}{4+3{m}^{2}}$��
��y0=-$\frac{3m}{4+3{m}^{2}}$��
��G��$\frac{4}{\sqrt{4+3{m}^{2}}}$��-$\frac{3m}{4+3{m}^{2}}$����
ֱ��OG�ķ���Ϊy=-$\frac{3m}{4}$x��������Բ���̵�x2=$\frac{16}{4+3{m}^{2}}$��
��B��$\frac{4}{\sqrt{4+3{m}^{2}}}$��-$\frac{3m}{\sqrt{4+3{m}^{2}}}$����
B��ֱ��AC�ľ���d1=$\frac{\sqrt{4+3{m}^{2}}-1}{\sqrt{1+{m}^{2}}}$��
O��ֱ��AC�ľ���d2=$\frac{1}{\sqrt{1+{m}^{2}}}$��
��SABCD=$\frac{1}{2}$|AC|��d1+d2��=6$\sqrt{\frac{1}{3}-\frac{1}{3��4+3{m}^{2}��}}$��3����m=0ʱȡ����Сֵ3��
���� ���⿼��켣���̣�����ֱ������Բ��λ�ù�ϵ���ۺ�Ӧ�ã���������ļ��㣬�����е��⣮

 ��һ����ͬ���ɽ�����ϵ�д�
��һ����ͬ���ɽ�����ϵ�д� ������Ӧ���ϵ�д�
������Ӧ���ϵ�д�| A�� | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{4}$=1 | B�� | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{3}$=1 | C�� | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1 | D�� | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1 |
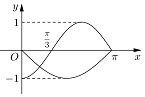 ��֪����y=f��x����ż������y=g��x�����溯�������ǵĶ�����Ϊ[-�У���]����������x��[0����]�ϵ�ͼ����ͼ��ʾ����ʽ$\frac{f��x��}{g��x��}��0$�Ľ⼯Ϊ$��-�У�-\frac{��}{3}���ȣ�0��\frac{��}{3}��$��
��֪����y=f��x����ż������y=g��x�����溯�������ǵĶ�����Ϊ[-�У���]����������x��[0����]�ϵ�ͼ����ͼ��ʾ����ʽ$\frac{f��x��}{g��x��}��0$�Ľ⼯Ϊ$��-�У�-\frac{��}{3}���ȣ�0��\frac{��}{3}��$��