题目内容
15．已知函数f（x）是偶函数，且在（0，+∞）上是减函数，证明：函数f（x）在（-∞，0）上是增函数．分析 根据题意，设-∞＜x1＜x2＜0，那么0＜-x2＜-x1＜+∞．由函数在（0，+∞）上的单调性可得f（-x2）＞f（-x1），结合偶函数的性质可得f（x1）＜f（x2）；由函数单调性的定义即可得证明．
解答 证明：设-∞＜x1＜x2＜0，那么0＜-x2＜-x1＜+∞．
由于偶函数在（0，+∞）上是减函数，故有：f（-x2）＞f（-x1）
又根据偶函数的性质可得：f（-x1）=f（x1），f（-x2）=f（x2）
综上可得：f（x1）＜f（x2）；
故f（x）在（-∞，0）上是减函数．
点评 本题主要考查函数奇偶性与单调性的综合问题，涉及函数单调性的证明，关键是运用偶函数的性质进行转化．
练习册系列答案
阅读快车系列答案
相关题目
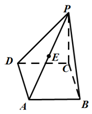如图在边长为2的菱形ABCD中，∠ABC=60°，PC⊥平面ABCD，PC=2，E为PA的中点．（1）求证：平面EBD⊥平面ABCD； 
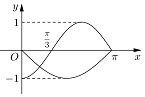已知函数y=f（x）是偶函数，y=g（x）的奇函数，它们的定义域为[-π，π]，且它们在x∈[0，π]上的图象如图所示，则不等式$\frac{f（x）}{g（x）}＞0$的解集为$（-π，-\frac{π}{3}）∪（0，\frac{π}{3}）$．
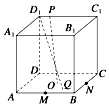在正方体ABCD-A1B1C1D1中，P为正方形A1B1C1D1四边上的动点，O为底面正方形ABCD的中心，M，N分别为AB，BC的中点，点Q为平面ABCD内一点，线段D1Q与OP互相平分，则满足$\overrightarrow{MQ}$=λ$\overrightarrow{MN}$的实数λ有2个．