题目内容
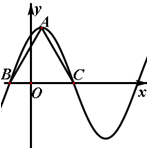 将形如
将形如
|
|
|
(1)求ω的值及函数f(x)的单调递增区间;
(2)若-2<f(x)-m<2,在x∈[0,2]上恒成立,求m的取值范围.
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,正弦函数的单调性
专题:三角函数的图像与性质
分析:(1)由条件求得函数f(x)的解析式,再利用正弦函数的单调性求得函数的增区间.
(2)依题意,
在x∈[0,2]时恒成立,即
.利用正弦函数的定义域和值域求得f(x)的值域,可得m的范围.
(2)依题意,
|
|
解答:
解:(1)由题意可得 f(x)=
=3cosωx+
sinωx
=2
(
cosωx+
sinωx)=2
sin(ωx+
),
故f(x)max=2
,∴BC=4,
=4,T=8=
,∴ω=
,∴f(x)=2
sin(
x+
).
令2kπ-
≤
x+
≤2kπ+
,k∈z,求得8k-
≤x≤8k+
,
故函数的单调递增区间:[-
+8k,
+8k],k∈Z.
(2)依题意,
在x∈[0,2]时恒成立,
∴
.
∵x∈[0,2],∴
x+
∈[
,
],sin(
x+
)∈[
,1],f(x)∈[
,2
].
∴m>2
-2,且 m<
+2,故要求的m的范围是(2
-2,
+2).
|
| 3 |
=2
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| π |
| 3 |
故f(x)max=2
| 3 |
| T |
| 2 |
| 2π |
| ω |
| π |
| 4 |
| 3 |
| π |
| 4 |
| π |
| 3 |
令2kπ-
| π |
| 2 |
| π |
| 4 |
| π |
| 3 |
| π |
| 2 |
| 10 |
| 3 |
| 2 |
| 3 |
故函数的单调递增区间:[-
| 10 |
| 3 |
| 2 |
| 3 |
(2)依题意,
|
∴
|
∵x∈[0,2],∴
| π |
| 4 |
| π |
| 3 |
| π |
| 3 |
| 5π |
| 6 |
| π |
| 4 |
| π |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
∴m>2
| 3 |
| 3 |
| 3 |
| 3 |
点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,正弦函数的单调性、函数的恒成立问题,正弦函数的定义域和值域,属于中档题.

练习册系列答案
相关题目
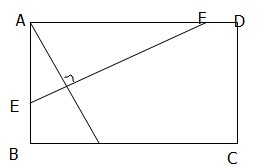 如图所示,已知正方形ABCD的边长为32cm,点P在BC上,且BP=16cm,EF⊥AP且与AB、CD分别相交于E、F两点,求EF的长.
如图所示,已知正方形ABCD的边长为32cm,点P在BC上,且BP=16cm,EF⊥AP且与AB、CD分别相交于E、F两点,求EF的长.