题目内容
已知四个半径为R的大球,上层一个,下层三个且两两相切叠放在一起,若在他们围成的空隙中,有一个小球与这四个大球都外切,另有一个更大的球与这四个球都内切,求小球的半径r1和更大球的半径r2.
考点:球的体积和表面积
专题:综合题,空间位置关系与距离
分析:我们易将这四个球的球心连接成一个正四面体,并根据四球外切,得到四面体的棱长为2R,正四面体的外接球半径为
R,由于这四个球之间有一个小球和这四个球都外切,则小球的球心与四面体的球体重合,进而再由小球与其它四球外切,球心距(即正四面体外接球半径)等于大球半径与小球半径之和,得到答案.
| ||
| 2 |
解答:
解:由已知中四个半径都是R的球中的三个放在桌面上,使它两两外切,
然后在它们上面放上第四个球,使它与前三个都相切,
连接四个球的球心,得到一个棱长为2R的正四面体
则该正四面体的外接球半径为
R
若这四个球之间有一个小球和这四个球都外切,则这个小球的半径为r1=(
-1)R,
另有一个更大的球与这四个球都内切,更大球的半径r2=(
+1)R.
然后在它们上面放上第四个球,使它与前三个都相切,
连接四个球的球心,得到一个棱长为2R的正四面体
则该正四面体的外接球半径为
| ||
| 2 |
若这四个球之间有一个小球和这四个球都外切,则这个小球的半径为r1=(
| ||
| 2 |
另有一个更大的球与这四个球都内切,更大球的半径r2=(
| ||
| 2 |
点评:本题考查的知识点是棱锥的结构特征,球的结构特征,其中根据已知条件求出四个半径为1的球球心连接后所形成的正四面体的棱长及外接球半径的长是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
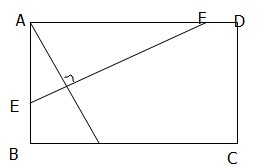 如图所示,已知正方形ABCD的边长为32cm,点P在BC上,且BP=16cm,EF⊥AP且与AB、CD分别相交于E、F两点,求EF的长.
如图所示,已知正方形ABCD的边长为32cm,点P在BC上,且BP=16cm,EF⊥AP且与AB、CD分别相交于E、F两点,求EF的长.