题目内容
设函数f（x）=x2+|x-2|-1，x∈R，则函数f（x）的最小值是 ．
考点：函数的最值及其几何意义
专题：计算题,函数的性质及应用
分析：写出分段函数，再求出函数f（x）的最小值．
解答：
解：f（x）=
，
由于f（x）在[2，+∞）上的最小值为f（2）=3，在（-∞，2）内的最小值为f(
)=
．
故答案为：
．
|
由于f（x）在[2，+∞）上的最小值为f（2）=3，在（-∞，2）内的最小值为f(
| 1 |
| 2 |
| 3 |
| 4 |
故答案为：
| 3 |
| 4 |
点评：本题考查函数的最值及其几何意义，确定分段函数是关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
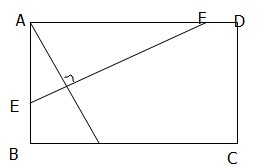如图所示，已知正方形ABCD的边长为32cm，点P在BC上，且BP=16cm，EF⊥AP且与AB、CD分别相交于E、F两点，求EF的长．