题目内容
某中学高一女生共有450人,为了了解高一女生的身高情况,随机抽取部分高一女生测量身高,所得数据整理后列出频率分布表如下:
(1)求出表中字母m、n、M、N所对应的数值;
(2)在给出的直角坐标系中画出频率分布直方图;
(3)估计该校高一女生身高在149.5~165.5cm范围内有多少人?
| 组别 | 频数 | 频率 |
| 145.5~149.5 | 8 | 0.16 |
| 149.5~153.5 | 6 | 0.12 |
| 153.5~157.5 | 14 | 0.28 |
| 157.5~161.5 | 10 | 0.20 |
| 161.5~165.5 | 8 | 0.16 |
| 165.5~169.5 | m | n |
| 合计 | M | N |
(2)在给出的直角坐标系中画出频率分布直方图;
(3)估计该校高一女生身高在149.5~165.5cm范围内有多少人?
考点:频率分布直方图,收集数据的方法
专题:概率与统计
分析:(I)在[145.5,149.5)这组数据中频率是0.16,频数是8,得到样本容量是M=
=50,进一步求出m,n,N
(II)根据频率分布表所给的分组和频率,做出频率分步直方图.
(III)由频率分布表中数据,可得高一女生身高在[155,165]的频率,根据做出的频率估计高一全体女生在这个区间的概率.
| 8 |
| 0.16 |
(II)根据频率分布表所给的分组和频率,做出频率分步直方图.
(III)由频率分布表中数据,可得高一女生身高在[155,165]的频率,根据做出的频率估计高一全体女生在这个区间的概率.
解答:
解 (1)由题意M=
=50,
落在区间165.5~169.5内数据频数m=50-(8+6+14+10+8)=4,
频率为n=
=0.08,总频率N=1.00.
(2)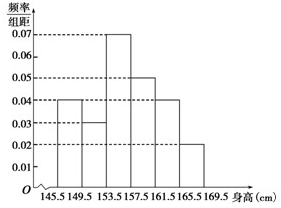
(3)该所学校高一女生身高在149.5~165.5 cm之间的比例为0.12+0.28+0.20+0.16=0.76,
则该校高一女生在此范围内的人数为450×0.76=342(人).
| 8 |
| 0.16 |
落在区间165.5~169.5内数据频数m=50-(8+6+14+10+8)=4,
频率为n=
| 4 |
| 50 |
(2)

(3)该所学校高一女生身高在149.5~165.5 cm之间的比例为0.12+0.28+0.20+0.16=0.76,
则该校高一女生在此范围内的人数为450×0.76=342(人).
点评:本题考查频率分步直方图的画法和应用,本题解题的关键是理解频率分步直方图中小长方形的面积是这组数据的频率,本题是一个基础题.

练习册系列答案
相关题目
设函数f(x)=2sin(2x+
),若f(x-φ)为偶函数,则φ可以为( )
| π |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设x,y满足
(a>1),若函数z=x+y取得最大值4,则实数a=( )
|
| A、2 | ||
| B、3 | ||
| C、4 | ||
D、
|