题目内容
5．已知集合A={x|x2-6x+8＜0}，B={x|（x-a）•（x-3a）＜0}．（1）若a=-1，求A∩（∁RB）；
（2）若A∩B=∅，求a的取值范围．
分析 （1）化简集合A，求出a=-1时的集合B以及∁RB，再计算A∩（∁RB）；
（2）讨论a的值，求出B对应的集合，从而得出满足A∩B=∅时a的取值范围．
解答 解：（1）∵集合A={x|x2-6x+8＜0}={x|2＜x＜4}，
a=-1时，B={x|（x+1）•（x+3）＜0}={x|-3＜x＜-1}，
∴∁RB={x|x≤-3或x≥-1}，
∴A∩（∁RB）={x|2＜x＜4}；
（2）当A∩B=∅时，
若a＞0，则B={x|a＜x＜3a}，须a≥4或3a≤2，
解得0＜a≤$\frac{2}{3}$或a≥4；
若a＜0时，B={x|3a＜x＜a}，须a≤2或a≥$\frac{4}{3}$；
解得a＜0时成立，验证当a=0时也成立；
综上，a≤$\frac{2}{3}$或a≥4时，A∩B=∅．
点评 本题考查了转化思想的应用，不等式组的解法，分类讨论思想的应用问题，是综合性题目．
练习册系列答案
相关题目
15．已知实数列{an}是等比数列，若a2a5a8=-8，则$\frac{1}{{a}_{1}{a}_{5}}$+$\frac{4}{{a}_{1}{a}_{9}}$+$\frac{9}{{a}_{5}{a}_{9}}$（ ）
| A． | 有最大值$\frac{1}{2}$ | B． | 有最小值$\frac{1}{2}$ | C． | 有最大值$\frac{5}{2}$ | D． | 有最小值$\frac{5}{2}$ |
14．
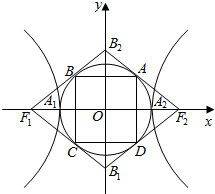我们把离心率为$\frac{\sqrt{5}+1}{2}$的双曲线叫做黄金双曲线．如图，黄金双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a，b＞0）的两顶点为A1，A2，虚轴两端点为B1，B2，两焦点为F1，F2，若以A1，A2为直径的圆内切于菱形F1B1F2B2，切点分别为A，B，C，D，则菱形F1B1F2B2的面积S1与矩形ABCD的面积S2的比值$\frac{{S}_{1}}{{S}_{2}}$=（ ）
我们把离心率为$\frac{\sqrt{5}+1}{2}$的双曲线叫做黄金双曲线．如图，黄金双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a，b＞0）的两顶点为A1，A2，虚轴两端点为B1，B2，两焦点为F1，F2，若以A1，A2为直径的圆内切于菱形F1B1F2B2，切点分别为A，B，C，D，则菱形F1B1F2B2的面积S1与矩形ABCD的面积S2的比值$\frac{{S}_{1}}{{S}_{2}}$=（ ）| A． | $\frac{\sqrt{5}+2}{2}$ | B． | $\frac{\sqrt{5}+1}{2}$ | C． | $\frac{\sqrt{5}-2}{2}$ | D． | $\frac{\sqrt{5}-1}{2}$ |