题目内容
若a,b,c为实数,且a<b<0,则下列命题正确的是( )
| A、ac2<bc2 | ||||
B、
| ||||
C、
| ||||
| D、a2>ab>b2 |
考点:不等式比较大小,不等关系与不等式
专题:不等式的解法及应用
分析:本题可以利用基本不等关系,判断选项中的命题是否正确,正确的可加以证明,错误的可以举反例判断,得到本题结论.
解答:
解:选项A,
∵c为实数,
∴取c=0,
ac2=0,bc2=0,
此时ac2=bc2,
故选项A不成立;
选项B,
-
=
,
∵a<b<0,
∴b-a>0,ab>0,
∴
>0,
即
>
,
故选项B不成立;
选项C,
∵a<b<0,
∴取a=-2,b=-1,
则
=
=
,
=2,
∴此时
<
,
故选项C不成立;
选项D,
∵a<b<0,
∴a2-ab=a(a-b)>0,
∴a2>ab.
∴ab-b2=b(a-b)>0,
∴ab>b2.
故选项D正确,
故选D.
∵c为实数,
∴取c=0,
ac2=0,bc2=0,
此时ac2=bc2,
故选项A不成立;
选项B,
| 1 |
| a |
| 1 |
| b |
| b-a |
| ab |
∵a<b<0,
∴b-a>0,ab>0,
∴
| b-a |
| ab |
即
| 1 |
| a |
| 1 |
| b |
故选项B不成立;
选项C,
∵a<b<0,
∴取a=-2,b=-1,
则
| b |
| a |
| -1 |
| -2 |
| 1 |
| 2 |
| a |
| b |
∴此时
| b |
| a |
| a |
| b |
故选项C不成立;
选项D,
∵a<b<0,
∴a2-ab=a(a-b)>0,
∴a2>ab.
∴ab-b2=b(a-b)>0,
∴ab>b2.
故选项D正确,
故选D.
点评:本题考查了基本不等关系,本题难度不大,属于基础题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
如图给出的是计算
+
+
+…+
的值的一个程序框图,其中判断框中应填入的是( )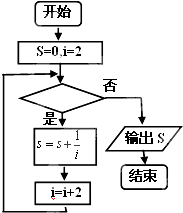
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 100 |

| A、i>100 | B、i≤100 |
| C、i>50 | D、i≤50 |
已知函数f(x)=lnx+2x-6,则它的零点所在的区间为( )
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
已知函数f(x)=
,其中a>0,x∈(0,b],则下列判断正确的是( )
| a+x2 |
| x |
A、当b>
| ||||
B、当0<b≤
| ||||
C、当0<b≤
| ||||
D、当b>0时,f(x)的最小值为2
|


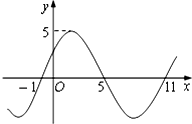 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0≤φ<2π)在R上的部分图象如图所示,则f(2014)=
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0≤φ<2π)在R上的部分图象如图所示,则f(2014)=