题目内容
已知函数y=f(2x+5)的定义域为[-2,2],则函数y=f(x)的定义域为 .
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:根据函数y=f(2x+5)的定义域为[-2,2]得自变量x满足:-2≤x≤2,所以可求得2x+5的范围,即为函数f(x)的定义域.
解答:
解:函数y=f(2x+5)的定义域为[-2,2],∴-2≤x≤2;
∴-4≤2x≤4,1≤2x+5≤9;
∴函数f(x)的定义域为[1,9],
故答案为:[1,9].
∴-4≤2x≤4,1≤2x+5≤9;
∴函数f(x)的定义域为[1,9],
故答案为:[1,9].
点评:本题主要考查复合函数定义域的求法,考查函数定义域的概念,并且要弄清定义域指的是自变量x的取值范围..

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若a,b,c为实数,且a<b<0,则下列命题正确的是( )
| A、ac2<bc2 | ||||
B、
| ||||
C、
| ||||
| D、a2>ab>b2 |
函数y=kx+b与函数y=
在同一坐标系中的大致图象正确的是( )
| kb |
| x |
A、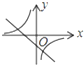 |
B、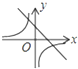 |
C、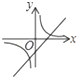 |
D、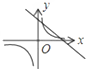 |
若曲线C1:x2+y2-8x=0与曲线C2:y(y-mx-m)=0有四个不同交点,则实数m的取值范围是( )
A、(-
| ||||
B、(-
| ||||
C、[-
| ||||
D、(-∞,-
|
已知甲、乙两地距丙的距离均为100km,且甲地在丙地的北偏东20°处,乙地在丙地的南偏东40°处,则甲乙两地的距离为( )
| A、100km | ||
| B、200km | ||
C、100
| ||
D、100
|
在钝角△ABC中,“sinA=
”是“∠A=
”的( )
| ||
| 2 |
| 2π |
| 3 |
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、非充分非必要条件 |